曲线的参数方程的定义：

一般地，在平面直角坐标系中，如果曲线C上任意一点的坐标x、y都是某个变数t的函数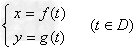①，并且对于t的每一个允许值，由方程组①所确定的点P（x，y）都在这条曲线C上，那么方程组①就叫做这条曲线的参数方程。变数t叫做参变量或参变数，简称参数。

曲线的参数方程的理解与认识：

（1）参数方程的形式：横、纵坐标x、y都是变量t的函数，给出一个t能唯一的求出对应的x、y的值，因而得出唯一的对应点；但横、纵坐标x、y之间的关系并不一定是函数关系。
（2）参数的取值范围：在表述曲线的参数方程时，必须指明参数的取值范围；取值范围的不同，所表示的曲线也可能会有所不同。
（3）参数方程与普通方程的统一性：普通方程是相对参数方程而言的，普通方程反映了坐标变量x与y之间的直接联系，而参数方程是通过变数反映坐标变量x与y之间的间接联系；普通方程和参数方程是同一曲线的两种不同表达形式；参数方程可以与普通方程进行互化。