本试题 “(1)计算:2cos245°+|2-2|-(12)-1(2)解不等式组:x+13≤13-4(x-1)<1(3)解方程:3x+2x2-x=2x-1.” 主要考查您对一元一次不等式组的解法
零指数幂(负指数幂和指数为1)
解分式方程
实数的运算
特殊角三角函数值
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 一元一次不等式组的解法
- 零指数幂(负指数幂和指数为1)
- 解分式方程
- 实数的运算
- 特殊角三角函数值
一元一次不等式组解集:
一元一次不等式组中各个不等式的解集的公共部分叫做这个不等式组的解集。
注:当任何数x都不能使各个不等式同时成立,我们就说这个一元一次不等式组无解或其解集为空集。
例如:
不等式x-5≤-1的解集为x≤4;
不等式x﹥0的解集是所有非零实数。
解法:求不等式组的解集的过程,叫做解不等式组。
求几个一元一次不等式的解集的公共部分,通常是利用数轴来确定的,公共部分是指数轴上被两条不等式解集的区域都覆盖的部分;
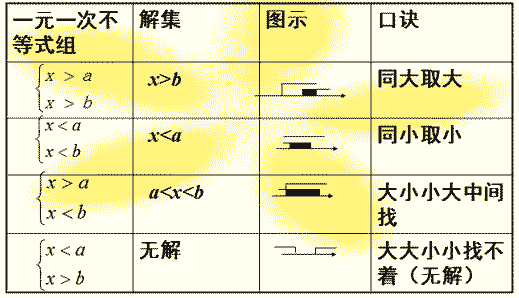
一般由两个一元一次不等式组成的不等式组由四种基本类型确定,它们的解集、数轴表示如下表:(设a<b)
一元一次不等式组的解答步骤:
(1)分别求出不等式组中各个不等式的解集;
(2)将这些不等式的解集在同一个数轴上表示出来,找出它们的的公共部分;
(3)根据找出的公共部分写出不等式组的解集,若没有公共部分,说明不等式组无解。
解法诀窍:
同大取大 ;
例如:
X>-1
X>2
不等式组的解集是X>2
同小取小;
例如:
X<-4
X<-6
不等式组的解集是X<-6
大小小大中间找;
例如,
x<2,x>1,不等式组的解集是1<x<2
大大小小不用找
例如,
x<2,x>3,不等式组无解
一元一次不等式组的整数解:
一元一次不等式组的整数解是指在不等式组中各个不等式的解集中满足整数条件的解的公共部分。
求一元一次不等式组的整数解的一般步骤:先求出不等式组的解集,再从解集中找出所有整数解,其中要注意整数解的取值范围不要搞错。
例如


所以原不等式的整数解为1,2。
负指数幂的定义:任何不等于零的数的-n(n为正整数)次幂,等于这个数的n次幂的倒数。
指数为1:任何不等于零的数的1次幂,所得结果都等于这个数的本身。
解分式方程的基本思想是把分式方程转化为整式方程,其一般步骤是:
(1)去分母:分式方程两边同乘以方程中各分母的最简公分母,把分式方程转化为整式方程。
(最简公分母:①系数取最小公倍数②出现的字母取最高次幂③出现的因式取最高次幂)
(2)解方程:解整式方程,得到方程的根;
(3)验根:将整式方程的解带入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;
否则,这个解不是原分式方程的解,是原分式方程的增根。
如果分式本身约分了,也要带进去检验。
在列分式方程解应用题时,不仅要检验所得解的是否满足方程式,还要检验是否符合题意。
一般的,解分式方程时,去分母后所得整式方程的解有可能使原方程中分母为零,因此要将整式方程的解代入最简公分母,如果最简公分母的值不为零,则是方程的解.
注意:
(1)注意去分母时,不要漏乘整式项。
(2)増根是分式方程去分母后化成的整式方程的根,但不是原分式方程的根。
(3)増根使最简公分母等于0。
分式方程的特殊解法:
换元法:
换元法是中学数学中的一个重要的数学思想,其应用非常广泛,当分式方程具有某种特殊形式,一般的去分母不易解决时,可考虑用换元法。
解分式方程的基本思路是将分式方程化为整式方程,具体做法是“去分母”,即方程两边同乘最简公分母,这也是解分式方程的一般思路和做法。
解分式方程注意:
①解分式方程的基本思想是把分式方程转化为整式方程,通过解整式方程进一步求得分式方程的解;
②用分式方程中的最简公分母同乘方程的两边,从而约去分母,但要注意用最简公分母乘方程两边各项时,切勿漏项;
③解分式方程可能产生使分式方程无意义的情况,那么检验就是解分式方程的必要步骤。
实数的运算:
实数包括有理数和无理数。其中无理数就是无限不循环小数,有理数就包括整数和分数。数学上,实数直观地定义为和数轴上的点一一对应的数。本来实数仅称作数,后来引入了虚数概念,原本的数称作“实数”——意义是“实在的数”。
实数可实现的基本运算有加、减、乘、除、乘方等,对非负数(即正数和0)还可以进行开方运算。实数加、减、乘、除(除数不为零)、平方后结果还是实数。任何实数都可以开奇次方,结果仍是实数,只有非负实数,才能开偶次方其结果还是实数。
四则运算封闭性:
实数集R对加、减、乘、除(除数不为零)四则运算具有封闭性,即任意两个实数的和、差、积、商(除数不为零)仍然是实数。
实数的运算法则:
1、加法法则:
(1)同号两数相加,取相同的符号,并把它们的绝对值相加;
(2)异号两数相加,取绝对值大的加数的符号,并用较大的绝对值减去较小的绝对值。
可使用
①加法交换律:两个数相加,交换加数的位置,和不变;即:a+b=b+a;
②加法结合律:三个数相加,先把前两个数相加,或先把后两个数相加,和不变;即:(a+b)+c=a+(b+c)。
2、减法法则:减去一个数等于加上这个数的相反数。即a-b=a+(-b)
3、乘法法则:
(1)两数相乘,同号取正,异号取负,并把绝对值相乘。
(2)n个实数相乘,有一个因数为0,积就为0;若n个非0的实数相乘,积的符号由负因数的个数决定,当负因数有偶数个时,积为正;当负因数为奇数个时,积为负。
(3)乘法可使用
①乘法交换律:两个数相乘,交换因数的位置,积不变,即:ab=ba;
②乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积不变,即:(ab)c=a(bc);
③分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加,即:a(b+c)=ab+ac。
4、除法法则:
(1)两数相除,同号得正,异号得负,并把绝对值相除。
(2)除以一个数等于乘以这个数的倒数。
(3)0除以任何数都等于0,0不能做被除数。
5、乘方:所表示的意义是n个a相乘,即an,正数的任何次幂是正数,负数的偶次幂是正数,负数的奇次幂是负数,乘方与开方互为逆运算。
实数的运算顺序:
乘方、开方为三级运算,乘、除为二级运算,加、减是一级运算,如果没有括号,在同一级运算中要从左到右依次运算,不同级的运算,先算高级的运算再算低级的运算,有括号的先算括号里的运算。无论何种运算,都要注意先定符号后运算。

与“(1)计算:2cos245°+|2-2|-(12)-1(2)解不等式组:x+13≤1...”考查相似的试题有:
- 不等式组-x<02x-1<0的解集是______.
- (12)0=______,(-15)0×3-2=______.
- 计算:(1)(2-1)0+(-12)-1-(-1)2011;(2)(y3x)2•(2y2-x)-2.
- 若(x-7)0=1,则x的取值范围为______.
- 解下列分式方程:(1)2x-3=5x+1;(2)11-x2=31-x-51+x.
- 若分式方程无解,则的值为 .
- (1)先化简,再求值:2a(a+b)-(a+b)2,其中a=3,b=5.(2)解方程:(x-1)2x2-x-1x-2=0.
- 计算(1)3-0.125-214+1.44;(2)π3- 5+ 22+ 514.(保留三位有效数字)
- (1)6cos30° ×tan30 °﹣2sin245 °=( );(2)﹣(π﹣1)0﹣2sin45°+tan45°=( )。
- 计算 .