本试题 “某学校为准备参加市运动会,对本校甲、乙两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm ),跳高成绩在175cm 以...” 主要考查您对分层抽样
频率分布表、频率分布直方图、频率分布折线图、茎叶图
众数、中位数、平均数
古典概型的定义及计算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 分层抽样
- 频率分布表、频率分布直方图、频率分布折线图、茎叶图
- 众数、中位数、平均数
- 古典概型的定义及计算
分层抽样:
当已知总体由差异明显的几部分组成时,常将总体分成几部分,然后按照各部分所占的比例进行抽样,这种抽样叫做分层抽样,其所分成的各个部分叫做层。
利用分层抽样抽取样本,每一层按照它在总体中所占的比例进行抽取。
不放回抽样和放回抽样:
在抽样中,如果每次抽出个体后不再将它放回总体,称这样的抽样为不放回抽样;如果每次抽出个体后再将它放回总体,称这样的抽样为放回抽样.
随机抽样、系统抽样、分层抽样都是不放回抽样
分层抽样的特点:
(1)分层抽样适用于差异明显的几部分组成的情况;
(2)在每一层进行抽样时,在采用简单随机抽样或系统抽样;
(3)分层抽样充分利用已掌握的信息,使样具有良好的代表性;
(4)分层抽样也是等概率抽样,而且在每层抽样时,可以根据具体情况采用不同的抽样方法,因此应用较为广泛。
常用的抽样方法及它们之间的联系和区别:
| 类别 | 共同点 | 各自特点 | 相互联系 | 适用范围 |
| 简单随机抽样 | 抽样过程中每个个体被抽取的概率是相同的 | 从总体中逐个抽取 | 总体中的个体个数少 | |
| 系统抽样 | 将总体均匀分成几个部分,按照事先确定的规则在各部分抽取 | 在起始部分抽样时采用简单随机抽样 | 总体中的个体个数多 | |
| 分层抽样 | 将总体分成几层,分层进行抽取 | 各层抽样时采用简单抽样或者相同抽样 | 总体由差异明显的几部分组成 |
频率分布:
样本中所有数据(或者数据组)的频率和样本容量的比就是该数据的频率,所有数据(或者数据组)的频率的分布变化规律叫做频率分布,可以用频率分布表,频率分布折线图,茎叶图,频率分布直方图来表示.
频率分布折线图:
如果将频率分布直方图中各相邻的矩形的上底边的中点顺次连接起,就得到一条折线,称这条折线为本组数据的频率折线图。
频数分布表:
反映总体频率分布的表格。
一般地,编制频率分布表的步骤如下:(1)求全距,决定组数和组距;(2)分组,通常对组内数值所在区间取左闭右开区间,最后一组取闭区间;(3)登记频数,计算频率,列出频率分布表。
茎叶图:
(1)茎是指中间的一列数,叶是从茎的旁边生长出来的数。
(2)制作茎叶图的方法是:将所有两位数的十位数字作为“茎”,个位数字作为“叶”,茎相同者共用一个茎,茎按从小到大的顺序从上向下列出,共茎的叶一般按从大到小(或从小到大)的顺序同行列出;
(3)茎叶图的性质: ①茎叶图的优点是保留了原始数据,便于记录及表示,能反映数据在各段上的分布情况。
②茎叶图不能直接反映总体的分布情况,这就需要通过茎叶图给出的数据求出数据的数字特征,进一步估计总体情况。
茎叶图的性质:
①茎叶图的优点是保留了原始数据,便于记录及表示,能反映数据在各段上的分布情况。
②茎叶图不能直接反映总体的分布情况,这就需要通过茎叶图给出的数据求出数据的数字特征,进一步估计总体情况。
作频率分布直方图的步骤:
①求极差,即一组数据中最大值和最小值的差。
②决定组距与组数.将数据分组时,组数应力求合适,以使数据的分布规律能较清楚的呈现出来。这时应注意:a.一般样本容量越大,所分组数越多;b.为方便起见,组距的选择应力求“取整”;c.当样本容量不超过100时,按照数据的多少,通常分成5组~l2组.
③将数据分组.
④计算各小组的频率(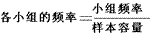 ),作频率分布表。
),作频率分布表。
⑤画频率分布直方图。
众数:
一组数据中,出现次数最多的数据叫做这组数据的众数。
中位数:
一组数据按大小依次排列,把处在最中间位置的一个数据(或中间两个数据的平均数)叫做这组数据的中位数。
平均数:
如果有几个数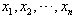 ,那么
,那么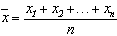 叫做这几个数的平均数。
叫做这几个数的平均数。
如果在几个数中,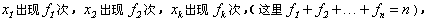 那么
那么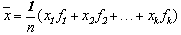 叫做这几个数的加权平均数。
叫做这几个数的加权平均数。
中位数的特点:
中位数不受少数几个极端值的影响,这在某些情况下是一个优点,但是它对极端值的不敏感有时也会成为缺点。
平均数、众数和中位数的作用:
平均数、众数和中位数都叫统计量,它们在统计中,有着广泛的应用。平均数、中位数、众数都是描述数据的集中趋势的“特征数”,平均数、中位数和众数从不同侧面给我们提供了同一组数据的面貌。
关于平均数、中位数、众数的选取:
(1)分析数据平中众,比较接近选平均,相差较大看中位,频数较大用众数;
(2)所有数据定平均,个数去除数据和,即可得到平均数;
(3)大小排列知中位;
(4)整理数据顺次排,单个数据取中问,双个数据两平均;频数最大是众数。
基本事件的定义:
一次试验连同其中可能出现的每一个结果称为一个基本事件。
等可能基本事件:
若在一次试验中,每个基本事件发生的可能性都相同,则称这些基本事件为等可能基本事件。
古典概型:
如果一个随机试验满足:(1)试验中所有可能出现的基本事件只有有限个;
(2)每个基本事件的发生都是等可能的;
那么,我们称这个随机试验的概率模型为古典概型.
古典概型的概率:
如果一次试验的等可能事件有n个,那么,每个等可能基本事件发生的概率都是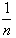 ;如果某个事件A包含了其中m个等可能基本事件,那么事件A发生的概率为
;如果某个事件A包含了其中m个等可能基本事件,那么事件A发生的概率为 。
。
古典概型解题步骤:
(1)阅读题目,搜集信息;
(2)判断是否是等可能事件,并用字母表示事件;
(3)求出基本事件总数n和事件A所包含的结果数m;
(4)用公式 求出概率并下结论。
求出概率并下结论。
求古典概型的概率的关键:
求古典概型的概率的关键是如何确定基本事件总数及事件A包含的基本事件的个数。
与“某学校为准备参加市运动会,对本校甲、乙两个田径队中30名跳...”考查相似的试题有:
- 某企业有3个分厂生产同一种电子产品,第一、二、三分厂的产量之比为1:2:1,用分层抽样方法(每个分厂的产品为一层)从3个分...
- 某工厂检查产品质量,抽查检验记录为一等品30件,二等品50件,三等品20件,则产品中三等品所占比例为( )A.0.125B.0.25C....
- 根据某市环境保护局公布2007-2012这六年每年的空气质量优良的天数,绘制折线图如图.根据图中信息可知,这六年的每年空气质量...
- 从2004个学生中选取50名组成参观团,若采用下面的方法选取;先用简单随机抽样从2004人中剔除4人,剩下2000人再安系统抽样的方...
- 某高校在2010 年的自主招生考试成绩中随机抽取100 名学生的笔试成绩,按成绩分组:第1 组,第2组,第3组,第4组,第5组,得到...
- 某学校为了了解学生的日平均睡眠时间(单位:h),随机选择了n名同学进行调查.下表是这n名同学的日睡眠时间的频率分布表,序号...
- 广州2010年亚运会火炬传递在A,B,C,D,E五个城市之间进行,各城市之间的距离(单位:百公里)见表.若以A为起点,E为终点,...
- 下图是2011年在某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数...
- 形如34021这样的数称为“波浪数”,即十位上的数字、千位上的数字均比与它们各自相邻的数字大,现从由0, 1, 2, 3, 4, 5组成的数...
- 从1,2,3,4,5,6这六个整数中任取两个数,下列叙述中是对立事件的是①恰有一个是偶数和恰有一个是奇数;②至少有一个是奇数和两个...