本试题 “如图,在6×8网格图中,每个小正方形边长均为1,点O和△ABC的顶点均在小正方形的格点上.(1)求△ABC的面积;(2)以O为位似中心,在网格图中作△A′B′C′和△ABC位...” 主要考查您对三角形的周长和面积
位似
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 三角形的周长和面积
- 位似
三角形的概念:
由不在同意直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
构成三角形的元素:
边:组成三角形的线段叫做三角形的边;
顶点:相邻两边的公共端点叫做三角形的顶点;
内角:相邻两边所组成的角叫做三角形的内角,简称三角形的角。
三角形有下面三个特性:
(1)三角形有三条线段;
(2)三条线段不在同一直线上;
(3)首尾顺次相接。
三角形的表示:
用符号“△,顶点是A、B、C的三角形记作“△ABC”,读作ABC”。
三角形的分类:
(1)三角形按边的关系分类如下:
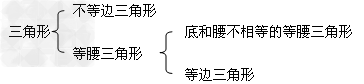 ;
;
(2)三角形按角的关系分类如下:

把边和角联系在一起,我们又有一种特殊的三角形:等腰直角三角形。它是两条直角边相等的直角三角形。
三角形的周长和面积:
三角形的周长等于三角形三边之和。
三角形面积=(底×高)÷2。
由不在同意直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
构成三角形的元素:
边:组成三角形的线段叫做三角形的边;
顶点:相邻两边的公共端点叫做三角形的顶点;
内角:相邻两边所组成的角叫做三角形的内角,简称三角形的角。
三角形有下面三个特性:
(1)三角形有三条线段;
(2)三条线段不在同一直线上;
(3)首尾顺次相接。
三角形的表示:
用符号“△,顶点是A、B、C的三角形记作“△ABC”,读作ABC”。
三角形的分类:
(1)三角形按边的关系分类如下:
 ;
;(2)三角形按角的关系分类如下:

把边和角联系在一起,我们又有一种特殊的三角形:等腰直角三角形。它是两条直角边相等的直角三角形。
三角形的周长和面积:
三角形的周长等于三角形三边之和。
三角形面积=(底×高)÷2。
位似图形:
如果两个图形不仅是相似图形,而且每组对应点的连线交于一点,那么这两个图形叫做位似图形。位似图形对应点连线的交点是位似中心,这时的相似比又称为位似比。
注:
①位似图形是相似图形的特例;
②位似图形一定是相似图形,但相似图形不一定是位似图形;
③位似图形的对应边互相平行或共线。
如果两个图形不仅是相似图形,而且每组对应点的连线交于一点,那么这两个图形叫做位似图形。位似图形对应点连线的交点是位似中心,这时的相似比又称为位似比。
注:
①位似图形是相似图形的特例;
②位似图形一定是相似图形,但相似图形不一定是位似图形;
③位似图形的对应边互相平行或共线。
位似图形的性质:
位似图形的任意一对对应点与位似中心在同一直线上,它们到位似中心的距离之比等于相似比。
1.位似图形对应线段的比等于相似比。
2.位似图形的对应角都相等。
3.位似图形对应点连线的交点是位似中心。
4.位似图形面积的比等于相似比的平方。
5.位似图形高、周长的比都等于相似比。
6.位似图形对应边互相平行或在同一直线上。
位似图形作用:
利用位似可以将一个图形任意放大或缩小。
位似图形的中心可以在任意的一点,不过位似图形也会随着位似中心的位变而位变。
根据一个位似中心可以作两个关于已知图形一定位似比的位似图形,这两个图形分布在位似中心的两侧,并且关于位似中心对称。
作图步骤:(位似比,即位似图形的相似比,指的是要求画的新图形与参照的原图形的相似比)
①首先确定位似中心,位似中心的位置可随意选择;
②确定原图形的关键点,如四边形有四个关键点,即它的四个顶点;
③确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小;
④符合要求的图形不惟一,因为所作的图形与所确定的位似中心的位置有关,并且同一个位似中心的两侧各有一个符合要求的图形,最好做两个。
位似变换:
把一个几何图形变换成与之位似的图形,叫做位似变换。
物理中的透镜成像就是一种位似变换,位似中心为光心。
位似变换应用极为广泛,特别是可以证明三点共线等问题。
发现相似题
与“如图,在6×8网格图中,每个小正方形边长均为1,点O和△ABC的顶...”考查相似的试题有:
- 如图,二次函数y=ax2的图象与一次函数y=x+b的图象相交于A(-2,2),B两点,从点A和点B分别引平行于y轴的直线与x轴分别交于C...
- 如图,长方形ABCD是由15个大小相等的正方形拼成的,每个正方形面积为1,E、F、G、H分别在AD、AB、BC、CD边上,且是某个小正方...
- 已知A(-4,0)、B(-2,3),则S△AOB=______.
- 在平面直角坐标系中,A(-5,0),B(3,0),点C在y轴上,△ABC的面积为12,求点C的坐标.
- 阅读材料:如下图(1)所示,在四边形ABCD中,对角线AC⊥BD于P,求证:S四边形ABCD=AC·BD。证明:AC⊥BD∴S四边形ABCD=S△ACD+S△A...
- 如图:直线y=kx+3与x轴、y轴分别交于A、B两点,tan∠OAB=,点C(x,y)是直线y=kx+3上与A、B不重合的动点。(1)求直线y=kx+3...
- 如图,在平面直角坐标系中,点A的坐标为(1,),△AOB的面积是。(1)求点B的坐标;(2)求过点A、O、B的抛物线的解析式;(3...
- 如图所示,请用两种位似的方法把四边形ABCD放大为原来的2倍。
- 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系。(1)点A的坐标为__...
- 如图,正五边形FGHMN是由正五边形ABCDE经过位似变换得到的,若AB:FG=2:3,则下列结论正确的是A.2DE=3MNB.3DE=2MNC.3∠A=2...