本试题 “有下列说法:①2的平方根是2;②5a与0.2a是同类二次根式;③2-1与2+1互为倒数;④3-2的绝对值是2-3.其中错误的是______(填序号).” 主要考查您对估算无理数的大小
平方根
同类二次根式
最简二次根式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 估算无理数的大小
- 平方根
- 同类二次根式
- 最简二次根式
在一些题目中我们常常需要估算无理数的取值范围,要想准确地估算出无理数的取值范围需要记住一些常用数的平方。一般情况下从1到达20整数的平方都应牢记。
例:估算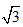 的取值范围。
的取值范围。
解:因为1<3<4,所以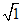 <
< <
< ,
,
即:1<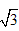 <2如果想估算的更精确一些,
<2如果想估算的更精确一些,
比如说想精确到0.1.可以这样考虑:因为17的平方是289,18的平方是324,所以1.7的平方是2.89,1.8的平方是3.24.
因为2.89<3<3.24,
所以 <
<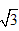 <
<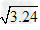 ,
,
所以1.7<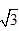 <1.8。
<1.8。
如果需要估算的数比较大,可以找几个比较接近的数值验证一下。
比较无理数大小的几种方法:
比较无理数大小的方法很多,在解题时,要根据所给无理数的特点,选择合适的比较方法。
一、直接法
直接利用数的大小来进行比较。
①、同是正数:
例: 与3的比较
与3的比较
根据无理数和有理数的联系,被开数大的那个就大。
因为3=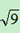 >
> ,所以3>
,所以3>
②、 同是负数:
根据无理数和有理数的联系,及同是负数绝对值大的反而小。
③、 一正一负:
正数大于一切负数。
二、隐含条件法:
根据二次根式定义,挖掘隐含条件。
例:比较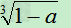 与
与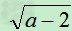 的大小。
的大小。
因为 成立
成立
所以a-2≧0即a≧2
所以1-a≦-1
所以 ≧0,
≧0,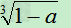 ≦-1
≦-1
所以 >
>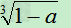
三、同次根式下比较被开方数法:
例:比较4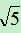 与5
与5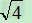 大小
大小
因为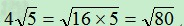
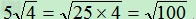
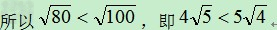
四、作差法:
若a-b>0,则a>b
例:比较3-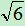 与
与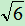 -2的大小
-2的大小
因为3-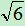 -
-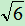 -2
-2
=3-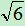 -
-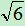 +2
+2
=5-2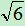
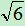 <
< =2.5
=2.5
所以:5-2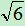 >0
>0
即3-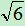 >
>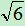 -2
-2
五、作商法:
a>0,b>0,若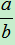 >1,则a>b
>1,则a>b
例:比较 与
与 的大小
的大小
因为 ÷
÷
= ×
×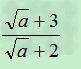
= <1
<1
所以: <
<
六、找中间量法
要证明a>b,可找中间量c,转证a>c,c>b
例:比较 与
与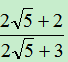 的大小
的大小
因为 >1,1>
>1,1>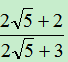
所以 >
>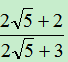
七、平方法:
a>0,b>0,若a2>b2,则a>b。
例:比较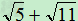 与
与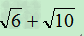 的大小
的大小
(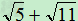 )2=5+2
)2=5+2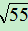 +11=16+2
+11=16+2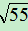
(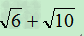 )2=6+2
)2=6+2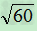 +10=16+2
+10=16+2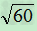
所以: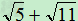 <
<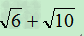
八、倒数法: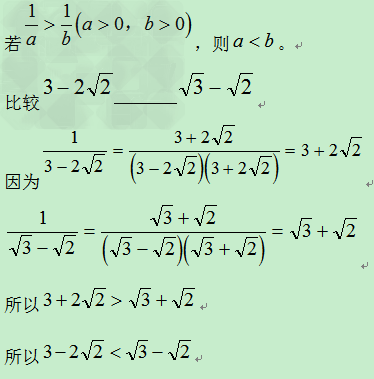
九、有理化法:
可分母有理化,也可分子有理化。 
十、放缩法:
常用无理数口诀记忆:
√2≈1.41421:意思意思而已
√3≈1.7320:一起生鹅蛋
√5≈2.2360679:两鹅生六蛋(送)六妻舅
√7≈2.6457513:二妞是我,气我一生
√8=2√2≈2.82842啊,不啊不是啊
e≈2.718:粮店吃一把
π≈3.14159,26535,897,932,384,262:
山巅一寺一壶酒,尔乐苦杀吾,把酒吃,酒杀尔,杀不死,尔乐尔
如果一个数的平方等于a,则这个数叫做a的平方根,如果x2=a,那么x叫做a的平方根,这里a是x的平方,它是一个非负数,即a≥0。
表示:一个正数有两个平方根,用
 表示平方根中正的那个,用-
表示平方根中正的那个,用-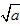 表示负的平方根。
表示负的平方根。性质:
①一个正数如果有平方根,那么必定有两个,它们互为相反数。
显然,如果我们知道了这两个平方根的一个,那么就可以及时的根据相反数的概念得到它的另一个平方根。
②如果一个正数x的平方等于a,即x的平方等于a,那么这个正数x叫做a的算术平方根。a
的算术平方根记为,读作“根号a”,a叫做被开方数。
③规定:0的平方根是0。
④负数在实数范围内不能开平方,只有在复数范围内,才可以开平方根。
例如:-1的平方根为±1,-9的平方根为±3。
⑤平方根包含了算术平方根,算术平方根是平方根中的一种。
平方根和算术平方根都只有非负数才有。
被开方数是乘方运算里的幂。
求平方根可通过逆运算平方来求。
开平方:求一个非负数a的平方根的运算叫做开平方,其中a叫做被开方数。
若x的平方等于a,那么x就叫做a的平方根,即正负根号a=正负x
1 至 20 的平方根:
利用长式除法可以求平方根。长式除法需要进行加法,减法,乘法,除法等四则运算。一般计算机软件的运算精度小于20位数字,如要计算平方根到100位,四则运算的精度需100位以上。 利用高精度长式除法可以计算出 1 至 20 的 平方根如下:
 |
=1 |
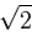 |
≈1.414213562373095048801688724209698078569671875376948073176679737990732478462 |
 |
≈1.732050807568877293527446341505872366942805253810380628055806979451933016909 |
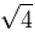 |
=2 |
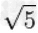 |
≈2.236067977499789696409173668731276235440618359611525724270897245410520925638 |
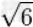 |
≈2.449489742783178098197284074705891391965947480656670128432692567250960377457 |
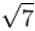 |
≈2.645751311064590590501615753639260425710259183082450180368334459201068823230 |
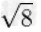 |
≈2.828427124746190097603377448419396157139343750753896146353359475981464956924 |
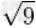 |
=3 |
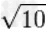 |
≈3.162277660168379331998893544432718533719555139325216826857504852792594438639 |
 |
≈3.316624790355399849114932736670686683927088545589353597058682146116484642609 |
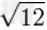 |
≈3.464101615137754587054892683011744733885610507620761256111613958903866033818 |
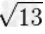 |
≈3.605551275463989293119221267470495946251296573845246212710453056227166948293 |
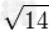 |
≈3.741657386773941385583748732316549301756019807778726946303745467320035156307 |
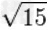 |
≈3.872983346207416885179265399782399610832921705291590826587573766113483091937 |
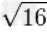 |
≈4 |
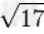 |
≈4.123105625617660549821409855974077025147199225373620434398633573094954346338 |
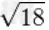 |
≈4.242640687119285146405066172629094235709015626130844219530039213972197435386 |
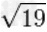 |
≈4.358898943540673552236981983859615659137003925232444936890344138159557328203 |
 |
≈4.472135954999579392818347337462552470881236719223051448541794490821041851276 |
其中,有两数的根号可借由“口诀”记忆:
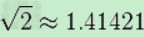 (意思意思而已),
(意思意思而已), (一妻三儿、一起散热)。
(一妻三儿、一起散热)。一个二次根式不能叫同类二次根式,至少两个二次根式才有可能称为同类二次根式。
要判断几个根式是不是同类二次根式,须先化简根号里面的数,把非最简二次根式化成最简二次根式,然后判断。
同类二次根式与同类项的异同:
同类二次根式与同类项无论在表现形式上还是运算法则上都有极类似之处,因此我们把二者的区别和联系列出,学习时注意辨析、对比来应用。
相同点
1. 两者都是两个代数式间的一种关系。同类项是两个单项间的关系,字母及相同字母的指数都相同的项;同类二次根式是两个二次根式间的关系,指化成最简二次根式后被开方数相同的二次根式。
2. 两者都能合并,而且合并法则相同。我们如果把最简二次根式的根号部分看做是同类项的指数部分,把根号外的因式看做是同类项的系数部分,那么同类二次根式的合并法则与同类项的合并法则相同,即“同类二次根式(或同类项)相加减,根式(字母)不变,系数相加减”。
不同点
1. 判断准则不同。
判断两个最简二次根式是否为同类二次根式,其依据是“被开方数是否相同”,与根号外的因式无关;而同类项的判断依据是“字母因式及其指数是否对应相同”,与系数无关。
2. 合并形式不同。
最简二次根式定义:
被开方数中不含字母,并且被开方数中所有因式的幂的指数都小于2,这样的二次根式称为最简二次根式。
有理化因式:两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,则说这两个代数式互为有理化因式。
最简二次根式同时满足下列三个条件:
(1)被开方数的因数是整数,因式是整式;
(2)被开方数中不含有能开的尽的因式;
(3)被开方数不含分母。
最简二次根式判定:
①在二次根式的被开方数中,只要含有分数或小数就不是最简二次根式;
②在二次根式的被开方数中的每一个因式(或因数),如果幂的指数等于或大于2,也不是最简二次根式。
化二次根式为最简二次根式的方法和步骤:
①如果被开方数是分数(包括小数)或分式,先利用商的算数平方根的性质把它写成分式的形式,然后利用分母有理化进行化简。
②如果被开方数是整数或整式,先将他们分解因数或因式,然后把能开得尽方的因数或因式开出来。
与“有下列说法:①2的平方根是2;②5a与0.2a是同类二次根式;③2-1...”考查相似的试题有:
- 下列运算正确的是( )A.B.C.a2a4=a8D.(﹣a3)2=a6
- 求下列各式的值:(1)(2)(3)(4)
- 49的平方根是( )。
- 观察下列各式及验证过程:……⑴按照上述三个等式及验证过程中的基本思想,猜想的变形结果并进行验证.⑵针对上述各式反映的规律...
- 下列各数中,与的积为有理数的是A.B.C.D.
- 下列各组二次根式中,化成最简二次根式后,被开方数相同的一组是( )A.2与75B.12与12C.3与27D.50与
- 若二次根式有意义,则x的取值范围是( )A.x≥1B.x>1C.x≥-1D.x≤1
- 最简二次根式的条件是(1)( );(2)( )
- 已知实数a、b满足条件|a-b|=ba<1,化简代数式(1a-1b)(a-b-1)2,将结果表示成只含有字母a的形式.
- 已知x=5-12,求代数式x3+2x2-1的值.