本试题 “国家对空气质量的分级规定如下表:污染指数0~5051~100101~150151~200201~300>300空气质量优良轻度污染中度污染重度污染严重污染某市去年6月份30天的空...” 主要考查您对离散型随机变量及其分布列
离散型随机变量的期望与方差
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 离散型随机变量及其分布列
- 离散型随机变量的期望与方差
随机变量:
随着试验结果变化而变化的变量,常用字母ξ,η等来表示随机变量。
离散型随机变量:
所有取值可以一一列出的随机变量;
离散型随机变量的分布列:
如果离散型随机变量ξ可能取的值为x1,x2,x3,…,xn,…,而ξ取每一个值xi(i=1,2,3,…)的概率P(ξ=xi)=pi,以表格的形式表示如下:

上表称为离散型随机变量ξ的概率分布列,简称为ξ的分布列。
任一随机变量的分布列都具有下列性质:
(1)0≤pi≤1,(i=1,2,3,…);
(2)p1+p2+p3+…+pn+…=1;
(3)离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和。
求离散型随机变量分布列:
(1)先判断一个变量是否为离散型随机变量,主要看变量的值能否按一定的顺序一一列举出来.
(2)明确随机变量X可取哪些值.
(3)求x取每一个值的概率.(4)列成分布列表,
数学期望的定义:
称 为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
方差的定义:
称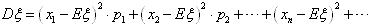 为ξ的均方差,简称为方差,
为ξ的均方差,简称为方差,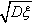 叫做随机变量ξ的标准差,记作:
叫做随机变量ξ的标准差,记作: 。
。
期望与方差的性质:
(1)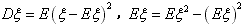 ;
;
(2)若η=aξ+b,则 ;
;
(3)若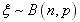 ,则
,则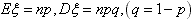 ;
;
(4)若ξ服从几何分布,则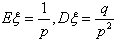 。
。
求均值(数学期望)的一般步骤:
(1)首先判断随机变量是否服从二点分布、二项分布或超几何分布,若服从,则直接用公式求均值.(2)若不服从特殊的分布,则先求出随机变量的分布列,再利用公式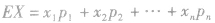 求均值。
求均值。
方差的求法:
(1)若随机变量X服从二点分布或二项分布,则直接利用方差公式可求.
(2)若随机变量X不服从特殊的分布时,求法为:
发现相似题
与“国家对空气质量的分级规定如下表:污染指数0~5051~100101~...”考查相似的试题有:
- 某车间在三天内,每天生产6件某产品,其中第一天、第二天、第三天分别生产出了2件、1件、1件次品,质检部门每天要从生产的6件...
- 一袋中装有分别标记着1,2,3,4数字的4只小球,每次从袋中取出一只球,设每只小球被取到的可能性相同.(1)若每次取出的球...
- 从“神七”飞船带回的某种植物种子由于在太空中被辐射,我们把它们称作“太空种子”。这种“太空种子”成功发芽的概率为,发生基因...
- 一批零件中有9个合格品与3个不合格品.安装机器时,从这批零件中任取一个.如果每次取出的不合格品不再放回去,求在取得合格...
- 某商场准备在伦敦奥运会期间举行促销活动.根据市场行情,该商场决定从3种品牌的服装类商品、2种品牌的家电类商品、4种品牌的...
- 如图,将一个各面都涂了油漆的正方体,切割成125个同样大小的小正方体.经过搅拌后,从中随机取出一个小正方体,记它的涂油漆...
- 某校要用三辆汽车从新校区把教职工接到老校区,已知从新校区到老校区有两条公路,汽车走①号公路堵车的概率为,不堵车的概率为...
- 抛掷一枚硬币5次,出现正面向上次数的数学期望为
- 设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6,且购买甲种商品与购买乙种商品相互独立,各顾...
- 已知某随机变量X的分布列如下(p,q∈R):X1-1Ppq且X的数学期望E(X)=12,那么X的方差D(X)=______.