本试题 “已知以F为焦点的抛物线y2=4x上的两点A、B满足AF=3FB,则弦AB的中点到准线的距离为______.” 主要考查您对点到直线的距离
抛物线的定义
抛物线的性质(顶点、范围、对称性、离心率)
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 点到直线的距离
- 抛物线的定义
- 抛物线的性质(顶点、范围、对称性、离心率)
点到直线的距离公式:
1、若点P(x0,y0)在直线Ax+By+C=0(A,B不同时为0)上,则Ax0+By0+C=0。
2、若点P(x0,y0)不在直线Ax+By+C=0(A,B不同时为0)上,则Ax0+By0+C≠0,此时点P(x0,y0)直线Ax+By+C=0(A,B不同时为0)的距离d= 。
。
点到直线的距离公式的理解:
①点到直线的距离是直线上的点与直线外一点的连线的最短距离(这是从运动观点来看的).
②若给出的直线方程不是一般式,则应先把方程化为一般式,再利用公式求距离.
③点到直线的距离公式适用于任何情况,其中点P在直线l上时,它到直线的距离为0.
④点到几种特殊直线的距离: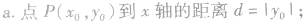
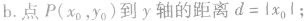
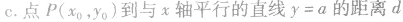

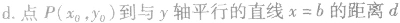
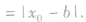
抛物线的定义:
平面内与一个定点F和一条定直线l(F∈l)的距离相等的点的轨迹叫做抛物线,定点F叫做抛物线的焦点,定直线l叫做抛物线的准线,抛物线的定义也可以说成是:平面内与一个定点F和一条定直线l的距离的比等于1的点的轨迹.
抛物线中的有关概念:
| 定义 | 图形 | |
| 抛物线的弦、焦点弦 | 连结抛物线上任意两点的线段,叫做抛物线的弦. 过抛物线焦点的弦,叫做焦点弦 |
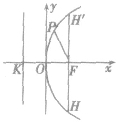 |
| 抛物线的通径和焦参数 | 过焦点且垂直于抛物线的弦叫做抛物线的通径,通径长度的一半叫做抛物线的焦参数 | |
| 焦点半径 | 抛物线上一点P和焦点的连线,叫做点P的焦点半径或焦半径 | |
| 抛物线的焦准距 | 抛物线的焦点和它的准线间的距离,叫做焦准距,依据定义,显然有KO=OF, 即焦准距等于通径长的一半,焦准距用常数p表示 即焦准距等于通径长的一半,焦准距用常数p表示 |
抛物线的规律总结:
①在抛物线的定义中的定点F不在直线l上,否则动点的轨迹就是过点F且垂直于直线l的一条直线,而不再是抛物线;
②抛物线的定义中指明了抛物线上的点到焦点的距离与到准线的距离相等,故在一些问题中,二者可以互相转化,这是利用抛物线定义解题的关键.
抛物线的性质(见下表):

抛物线的焦点弦的性质:

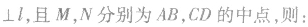

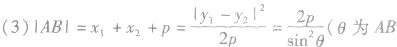

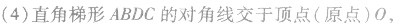


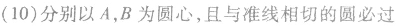
关于抛物线的几个重要结论:
(1)弦长公式同椭圆.
(2)对于抛物线y2=2px(p>0),我们有P(x0,y0)在抛物线内部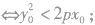 P(x0,y0)在抛物线外部
P(x0,y0)在抛物线外部
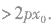
(3)抛物线y2=2px上的点P(x1,y1)的切线方程是 抛物线y2=2px(p>0)的斜率为k的切线方程是y=kx+
抛物线y2=2px(p>0)的斜率为k的切线方程是y=kx+
(4)抛物线y2=2px外一点P(x0,y0)的切点弦方程是
(5)过抛物线y2=2px上两点
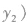 的两条切线交于点M(x0,y0),则
的两条切线交于点M(x0,y0),则
(6)自抛物线外一点P作两条切线,切点为A,B,若焦点为F,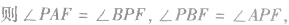 又若切线PA⊥PB,则AB必过抛物线焦点F.
又若切线PA⊥PB,则AB必过抛物线焦点F.
利用抛物线的几何性质解题的方法:
根据抛物线定义得出抛物线一个非常重要的几何性质:抛物线上的点到焦点的距离等于到准线的距离.利用抛物线的几何性质,可以进行求值、图形的判断及有关证明.
抛物线中定点问题的解决方法:
在高考中一般以填空题或选择题的形式考查抛物线的定义、标准方程以及几何性质等基础知识,在解答题中常常将解析几何中的方法、技巧与思想集于一身,与其他圆锥曲线或其他章节的内容相结合,考查综合分析问题的能力,而与抛物线有关的定值及最值问题是一个很好的切人点,充分利用点在抛物线上及抛物线方程的特点是解决此类题型的关键,在求最值时经常运用基本不等式、判别式以及转化为函数最值等方法。
利用焦点弦求值:
利用抛物线及焦半径的定义,结合焦点弦的表示,进行有关的计算或求值。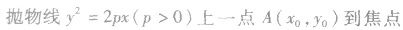
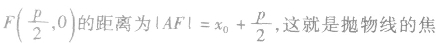
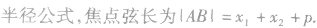
与“已知以F为焦点的抛物线y2=4x上的两点A、B满足AF=3FB,则弦AB...”考查相似的试题有:
- 原点到直线x+2y-=0的距离为[ ]A.1B.C.2D.
- 已知圆上有两点且满足,则直线的方程为____________________.
- 若不同两点P,Q的坐标分别为(a,b),(3-b,3-a),则线段PQ的垂直平分线l的斜率为 ,圆(x-2)2+(y-3)2=1关于直线对称的圆...
- 一条直线过点P(-3,-32),且圆x2+y2=25的圆心到该直线的距离为3,则该直线的方程为( )A.x=-3或3x+4y+15=0B.x=-3或y=-32...
- (本小题满分12分)如图,已知圆经过椭圆的右焦点F及上顶点B.过点作倾斜角为的直线交椭圆于C、D两点.(1)求椭圆的方程;(...
- 已知圆交于A、B两点,则AB所在的直线方程是____________________。
- (文)已知过抛物线的焦点的直线交该抛物线于、两点,,则___________ .
- 设抛物线上一点P到直线的距离是5,则点P到抛物线焦点F的距离为
- 已知抛物线y=x2上有一定点A(-1,1)和两动点P、Q,当PA⊥PQ时,点Q的横坐标取值范围是( )A.(-∞,-3]B.[1,+∞)C.[-3,1...
- 若抛物线y2=2px的焦点与椭圆的右焦点重合,则实数p的值是( )