本试题 “某公司共有职工8000名,从中随机抽取了100名,调查上、下班乘车所用时间,得下表:所用时间(分钟)[0,20)[20,40)[40,60)[60,80)[80,100)人数25501...” 主要考查您对频率分布表、频率分布直方图、频率分布折线图、茎叶图
随机事件及其概率
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 频率分布表、频率分布直方图、频率分布折线图、茎叶图
- 随机事件及其概率
频率分布:
样本中所有数据(或者数据组)的频率和样本容量的比就是该数据的频率,所有数据(或者数据组)的频率的分布变化规律叫做频率分布,可以用频率分布表,频率分布折线图,茎叶图,频率分布直方图来表示.
频率分布折线图:
如果将频率分布直方图中各相邻的矩形的上底边的中点顺次连接起,就得到一条折线,称这条折线为本组数据的频率折线图。
频数分布表:
反映总体频率分布的表格。
一般地,编制频率分布表的步骤如下:(1)求全距,决定组数和组距;(2)分组,通常对组内数值所在区间取左闭右开区间,最后一组取闭区间;(3)登记频数,计算频率,列出频率分布表。
茎叶图:
(1)茎是指中间的一列数,叶是从茎的旁边生长出来的数。
(2)制作茎叶图的方法是:将所有两位数的十位数字作为“茎”,个位数字作为“叶”,茎相同者共用一个茎,茎按从小到大的顺序从上向下列出,共茎的叶一般按从大到小(或从小到大)的顺序同行列出;
(3)茎叶图的性质: ①茎叶图的优点是保留了原始数据,便于记录及表示,能反映数据在各段上的分布情况。
②茎叶图不能直接反映总体的分布情况,这就需要通过茎叶图给出的数据求出数据的数字特征,进一步估计总体情况。
茎叶图的性质:
①茎叶图的优点是保留了原始数据,便于记录及表示,能反映数据在各段上的分布情况。
②茎叶图不能直接反映总体的分布情况,这就需要通过茎叶图给出的数据求出数据的数字特征,进一步估计总体情况。
作频率分布直方图的步骤:
①求极差,即一组数据中最大值和最小值的差。
②决定组距与组数.将数据分组时,组数应力求合适,以使数据的分布规律能较清楚的呈现出来。这时应注意:a.一般样本容量越大,所分组数越多;b.为方便起见,组距的选择应力求“取整”;c.当样本容量不超过100时,按照数据的多少,通常分成5组~l2组.
③将数据分组.
④计算各小组的频率(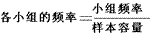 ),作频率分布表。
),作频率分布表。
⑤画频率分布直方图。
随机事件的定义:
在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件叫做随机事件,随机事件通常用大写英文字母A、B、C等表示。
必然事件的定义:
必然会发生的事件叫做必然事件;
不可能事件:
肯定不会发生的事件叫做不可能事件;
概率的定义:
在大量进行重复试验时,事件A发生的频率 总是接近于某个常数,在它附近摆动。这时就把这个常数叫做事件A的概率,记作P(A)。
总是接近于某个常数,在它附近摆动。这时就把这个常数叫做事件A的概率,记作P(A)。
m,n的意义:事件A在n次试验中发生了m次。
因0≤m≤n,所以,0≤P(A)≤1,必然事件的概率为1,不可能发生的事件的概率0。
随机事件概率的定义:
对于给定的随机事件A,随着试验次数的增加,事件A发生的频率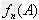 总是接近于区间[0,1]中的某个常数,我们就把这个常数叫做事件A的概率,记作P(A)。
总是接近于区间[0,1]中的某个常数,我们就把这个常数叫做事件A的概率,记作P(A)。
频率的稳定性:
即大量重复试验时,任何结果(事件)出现的频率尽管是随机的,却“稳定”在某一个常数附近,试验的次数越多,频率与这个常数的偏差大的可能性越小,这一常数就成为该事件的概率;
“频率”和“概率”这两个概念的区别是:
频率具有随机性,它反映的是某一随机事件出现的频繁程度,它反映的是随机事件出现的可能性;概率是一个客观常数,它反映了随机事件的属性。
与“某公司共有职工8000名,从中随机抽取了100名,调查上、下班乘...”考查相似的试题有:
- 一个容量为n的样本,分成若干组,已知某组频数和频率分别为36和0.25,则n=______.
- 为了检测某种产品的直径(单位mm),抽取了一个容量为100的样本,其频率分布表(不完整)如下:分组频数累计频数频率[10.75,...
- 一袋中装有5个白球,3个红球,现从袋中往外取球,每次取出一个,取出后记下球的颜色,然后放回,直到红球出现2次停止,用X表...
- (本小题满分12分)在平面直角坐标系中,点M的坐标为(x,y),点P的坐标为(2,3).(I)在一个密封的盒子中,放有标号为1,...
- 质检部门将对12个厂家生产的婴幼儿奶粉进行质量抽检,若被抽检厂家的奶粉经检验合格,则该厂家的奶粉即可投放市场;若检验不...
- 已知六条桥梁横跨A、B两岸,假设各条桥梁的车流量分别为1,1,2,2,3,4(单位万辆),现从这六条桥梁中任取三条桥梁,考察这三条...
- 奇瑞公司生产的“奇瑞”轿车是我国民族汽车品牌.该公司2009年生产的“旗云”、“风云”、“”三类经济型轿车中,每类轿车均有舒适和标...
- 一个口袋中装有大小相同的2个白球和3个黑球,从中摸出一个球,放回后再摸出一个球,则两次摸出的球恰好颜色不同的概率为______.
- 某次文艺汇演中共有9个展演节目,其中有两个是歌舞类节目,现随机安排演出表,则出现歌舞类节目即不在第一个,也不在最后一个...
- 一个袋中装有2个红球和2个白球,现从袋中取出1球,然后放回袋中再取出一球,则取出的两个球同色的概率为( )A.12B.13C.14...