本试题 “一位射击选手以往1000发子弹的射击结果统计如下表:环数1098765频数2503502001305020假设所打环数只取整数,试根据以上统计数据估算:(1)设该选手一次射击...” 主要考查您对n次独立重复试验
离散型随机变量的期望与方差
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- n次独立重复试验
- 离散型随机变量的期望与方差
独立重复试验:
(1)独立重复试验的意义:做n次试验,如果它们是完全同样的一个试验的重复,且它们相互独立,那么这类试验叫做独立重复试验.
(2)一般地,在n次独立重复试验中,设事件A发生的次数为X,在每件试验中事件A发生的概率为p,那么在n次独立重复试验中,事件A恰好发生k次的概率为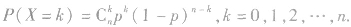 此时称随机变量X服从二项分布,记作
此时称随机变量X服从二项分布,记作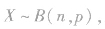 并称p为成功概率.
并称p为成功概率.
(3)独立重复试验:若n次重复试验中,每次试验结果的概率都不依赖于其他各次试验的结果,则称这n次试验是独立的.
(4)独立重复试验概率公式的特点: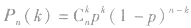 是n次独立重复试验中某 事件A恰好发生k次的概率.其中,n是重复试验的次数,p是一次试验中某事件A发生的概率,k是在n次独立重复试验中事件A恰好发生的次数,需要弄清公式中n,p,k的意义,才能正确运用公式.
是n次独立重复试验中某 事件A恰好发生k次的概率.其中,n是重复试验的次数,p是一次试验中某事件A发生的概率,k是在n次独立重复试验中事件A恰好发生的次数,需要弄清公式中n,p,k的意义,才能正确运用公式.
求独立重复试验的概率:
(1)在n次独立重复试验中,“在相同条件下”等价于各次试验的结果不会受其他试验的影响,即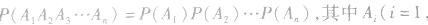 2,…,n)是第i次试验的结果.
2,…,n)是第i次试验的结果.
(2)独立重复试验是相互独立事件的特例,只要有“恰好”“恰有”字样的用独立重复试验的概率公式计算更简单,要弄清n,p,k的意义。
数学期望的定义:
称 为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
方差的定义:
称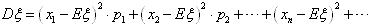 为ξ的均方差,简称为方差,
为ξ的均方差,简称为方差,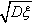 叫做随机变量ξ的标准差,记作:
叫做随机变量ξ的标准差,记作: 。
。
期望与方差的性质:
(1)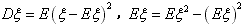 ;
;
(2)若η=aξ+b,则 ;
;
(3)若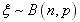 ,则
,则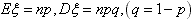 ;
;
(4)若ξ服从几何分布,则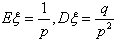 。
。
求均值(数学期望)的一般步骤:
(1)首先判断随机变量是否服从二点分布、二项分布或超几何分布,若服从,则直接用公式求均值.(2)若不服从特殊的分布,则先求出随机变量的分布列,再利用公式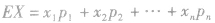 求均值。
求均值。
方差的求法:
(1)若随机变量X服从二点分布或二项分布,则直接利用方差公式可求.
(2)若随机变量X不服从特殊的分布时,求法为:
与“一位射击选手以往1000发子弹的射击结果统计如下表:环数10987...”考查相似的试题有:
- 某公司在开发的初级阶段大量生产一种产品.这种产品是否合格要进行A、B两项技术指标检测,设各项技术指标达标与否互不影响....
- (本小题满分12分)一射击测试每人射击三次,每击中目标一次记10分。没有击中记0分,某人每次击中目标的概率为(I)求此人得2...
- (理科)若随机变量ξ~N(2,22),则D(14ξ)的值为______.
- 某单位有三辆汽车参加某种事故保险,单位年初向保险公司缴纳每辆900元的保险金、对在一年内发生此种事故的每辆汽车,单位获90...
- 2008年10月10日至15日,孝感市第三届运动会胜利召开.在安全保障方面,警方从警犬训练基地挑选防暴犬时,从体能、嗅觉、反应...
- 甲、乙二人进行一次围棋比赛,约定先胜局者获得这次比赛的胜利,比赛结束.假设在一局比赛中,甲获胜的概率为,乙获胜的概率...
- (本小题满分12分)在一次人才招聘会上,有三种不同的技工面向社会招聘,已知某技术人员应聘三种技工被录用的概率分别是0.8、...
- 袋中装有10个大小相同的小球,其中黑球3个,白球n个(4≤n≤6) ,其余均为红球。(1)从袋中一次任取2个球,如果这2个球颜色相...
- (本小题12分)为丰富高三学生的课余生活,提升班级的凝聚力,某校高三年级6个班(含甲、乙)举行唱歌比赛.比赛通过随机抽签...
- 某学校举行知识竞赛,第一轮选拔共设有A、B、C、D四个问题,规则如下:①每位参加者计分器的初始分均为10分,答对问题A、B、C...