本试题 “计算.(1)(2)(3)(x+3)3+125=0(求x的值)” 主要考查您对二次根式的乘除
二次根式的加减
立方根
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 二次根式的乘除
- 二次根式的加减
- 立方根
二次根式的乘除法则:
1、二次根式的乘法原则: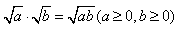 ,即两个二次根式相乘,根指数不变,相乘的结果是一个二次根式或有理式。
,即两个二次根式相乘,根指数不变,相乘的结果是一个二次根式或有理式。
2、二次根式的除法原则: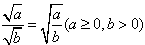 ,即二次根式相除,就是把被被开方数相除,根指数不变。
,即二次根式相除,就是把被被开方数相除,根指数不变。
有理化根式:如果两个含有根式的代数式的积不再含有根式,那么这两个代数式叫做有理化根式,也称有理化因式。
1、二次根式的乘法原则:
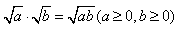 ,即两个二次根式相乘,根指数不变,相乘的结果是一个二次根式或有理式。
,即两个二次根式相乘,根指数不变,相乘的结果是一个二次根式或有理式。 2、二次根式的除法原则:
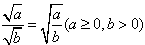 ,即二次根式相除,就是把被被开方数相除,根指数不变。
,即二次根式相除,就是把被被开方数相除,根指数不变。 有理化根式:如果两个含有根式的代数式的积不再含有根式,那么这两个代数式叫做有理化根式,也称有理化因式。
二次根式加减法法则:
先把式子中各项二次根式化成最简二次根式,然后再合并同类二次根式。
1、同类二次根式
一般地,把几个二次根式化为最简二次根式后,如果它们的被开方数相同,就把这几个二次根式叫做同类二次根式。
2、合并同类二次根式
把几个同类二次根式合并为一个二次根式就叫做合并同类二次根式。
3、二次根式加减时,可以先将二次根式化为最简二次根式,再将被开方数相同的进行合并。
例如:(1);2 +3
+3 =5
=5 (2)
(2)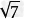 +2
+2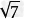 =3
=3
4、注意:有括号时,要先去括号。
二次根式的加减注意:
①二次根式合并同类项与合并同类项类似,因此二次根式的加减可以对比整式的加减进行;
②二次根式加减混合运算的是指就是合并同类项二次根式,不是同类二次根式不能合并。如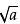 +
+ 是最简结果,不能再合并;
是最简结果,不能再合并;
③二次根式进行加减运算时,根号外的系数因式须保留假分数形式,如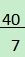
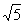 ,不能写成5
,不能写成5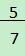
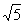
④合并同类二次根式后若系数为多项式,须添加括号。
先把式子中各项二次根式化成最简二次根式,然后再合并同类二次根式。
1、同类二次根式
一般地,把几个二次根式化为最简二次根式后,如果它们的被开方数相同,就把这几个二次根式叫做同类二次根式。
2、合并同类二次根式
把几个同类二次根式合并为一个二次根式就叫做合并同类二次根式。
3、二次根式加减时,可以先将二次根式化为最简二次根式,再将被开方数相同的进行合并。
例如:(1);2
 +3
+3 =5
=5 (2)
(2)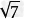 +2
+2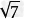 =3
=3
4、注意:有括号时,要先去括号。
二次根式的加减注意:
①二次根式合并同类项与合并同类项类似,因此二次根式的加减可以对比整式的加减进行;
②二次根式加减混合运算的是指就是合并同类项二次根式,不是同类二次根式不能合并。如
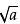 +
+ 是最简结果,不能再合并;
是最简结果,不能再合并;③二次根式进行加减运算时,根号外的系数因式须保留假分数形式,如
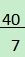
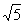 ,不能写成5
,不能写成5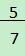
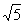
④合并同类二次根式后若系数为多项式,须添加括号。
定义:
一般地,如果一个数x的立方等于a,那么这个x叫做a的立方根。
如果一个数x的立方等于a,即x的三次方等于a(x3=a),即3个x连续相乘等于a,那么这个数x就叫做a的立方根,也叫做三次方根。
数a的立方根记作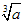 ,读作“三次根号a”。
,读作“三次根号a”。
读作:“三次根号a”其中,a叫做被开方数,3叫做根指数。(a等于所有数,包括0)如果被开方数还有指数,那么这个指数(必须是三能约去的)还可以和三次根号约去。
平方根和立方根的关系:
区别:
⑴根指数不同:平方根的根指数为2,且可以省略不写;立方根的根指数为3,且不能省略不写。
⑵ 被开方的取值范围不同:平方根中被开方数必需为非负数;立方根中被开方数可以为任何数。
⑶ 结果不同:平方根的结果除0之外,有两个互为相反的结果;立方根的结果只有一个。
联系:
二者都是与乘方运算互为逆运算
在部分科学计算器上面需要按SHIFT键+x3才可以打出来根号。
一般地,如果一个数x的立方等于a,那么这个x叫做a的立方根。
如果一个数x的立方等于a,即x的三次方等于a(x3=a),即3个x连续相乘等于a,那么这个数x就叫做a的立方根,也叫做三次方根。
数a的立方根记作
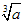 ,读作“三次根号a”。
,读作“三次根号a”。读作:“三次根号a”其中,a叫做被开方数,3叫做根指数。(a等于所有数,包括0)如果被开方数还有指数,那么这个指数(必须是三能约去的)还可以和三次根号约去。
开立方:求一个数a的立方根的运算叫做开立方,其中a叫做被开方数。
立方根性质:
①正数的立方根是正数;负数的立方根是负数;0的立方根是0。
②一般地,如果一个数X的立方等于 a,那么这个数X就叫做a的立方根(也叫做三次方根)。
也就是说,如果x3=a,那么x叫做a的立方根。
如2是8的立方根,-3分之2是-27分之8的立方根,0是0的立方根。
③立方和开立方运算,互为逆运算。
④互为相反数的两个数的立方根也是互为相反数。
⑤负数不能开平方,但能开立方。
⑥任何数(正数、负数、或零)的立方根如果存在的话,必定只有一个。
⑦当两个数相等时,这两个数的平方根相等,反之亦然。
平方根和立方根的关系:
区别:
⑴根指数不同:平方根的根指数为2,且可以省略不写;立方根的根指数为3,且不能省略不写。
⑵ 被开方的取值范围不同:平方根中被开方数必需为非负数;立方根中被开方数可以为任何数。
⑶ 结果不同:平方根的结果除0之外,有两个互为相反的结果;立方根的结果只有一个。
联系:
二者都是与乘方运算互为逆运算
在部分科学计算器上面需要按SHIFT键+x3才可以打出来根号。
笔算开立方的方法:
方法一
1.将被开立方数的整数部分从个位起向左每三位分为一组;
2.根据最左边一组,求得立方根的最高位数;
3.用第一组数减去立方根最高位数的立方,在其右边写上第二组数;
4.用求得的最高位数的平方的300倍试除上述余数,得出试商;并把求得的最高位数的平方的300倍与试商的积、求得的最高位数的30倍与试商的平方的积和试商的立方写在竖式左边,观察其和是否大于余数,若大于,就减小试商再试,若不大于,试商就是立方根的第二位数;
5.用同样方法继续进行下去。
方法二
第1、2步同上。
第三步,商完后,落下余数和后面紧跟着的三位,如果后面没有就把余数后面添上三个0;
第四步,将要试商的数代入式子“已商数×要试商数×(10×已商数+要试商数)×30+要商数的立方”,最接近但不超过第三步得到的数者,即为这一位要商的数。
然后重复第3、4步,直到除尽。
发现相似题
与“计算.(1)(2)(3)(x+3)3+125=0(求x的值)”考查相似的试题有:
- 直接写出计算结果:(1) ;(2) (m>1).
- 已知 .
- 下列计算正确的是( ) A.+= B.-=1 C.÷=2 D.×=
- 函数中,自变量的取值范围是 .
- 设[x]表示最接近x的整数(x≠n+0.5,n为整数),则[ ]A.131B.146C.161D.666
- 将1、、、按右侧方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,7)表示的两数之积是 .
- 计算:(1)32-218+0.5;(2)(3+5)(3-5)-(3-1)2.
- 要使代数式有意义,x的取值范围满足( )A.B.x≠2C.x>2D.x<2
- 计算:-ˉ
- 如果一个数的平方根与立方根相同,则这个数为[ ]A.0B.1C.0或1D.0或±1