本试题 “在△ABC,∠C=90°,斜边AB=10,直角边AC、BC的长是关于x的方程x2-mx+3m+6=0的两个实数根.(1)求m的值;(2)计算sinA+sinB+sinA•sinB.” 主要考查您对一元二次方程根与系数的关系
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 一元二次方程根与系数的关系
一元二次方程根与系数的关系:
如果方程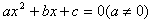 的两个实数根是
的两个实数根是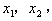 那么
那么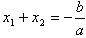 ,
,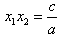 。
。
也就是说,对于任何一个有实数根的一元二次方程,两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商。
如果方程
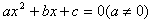 的两个实数根是
的两个实数根是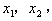 那么
那么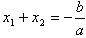 ,
,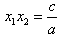 。
。也就是说,对于任何一个有实数根的一元二次方程,两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商。
一元二次方程根与系数关系的推论:
1.如果方程x2+px+q=0的两个根是x1、x2,那么x1+x2=-p , x1`x2=q
2.以两个数x1、x2为根的一元二次方程(二次项系数为1)是x2-(x1+x2)x+x1x2=0
提示:
①运用根与系数的关系和运用根的判别式一样,都必须先把方程化为一般形式,以便正确确定a、b、c的值。
②有推论1可知,对于二次项系数为1的一元二次方程,他的两根之和等于一次项系数的相反数,两根之积等于常数项。
③推论2可以看作推论1的逆定理,利用推论2可以直接求出以两个数x1、x2为根的一元二次方程(二次项系数是1)是x2-(x1+x2)x+x1x2=0
发现相似题
与“在△ABC,∠C=90°,斜边AB=10,直角边AC、BC的长是关于x的方程x...”考查相似的试题有:
- 若关于x的一元二次方程x2+(k+3)x+k=0的一个根是-2,则另一个根是( )A.2B.1C.-1D.0
- 方程x2-3x+7=0的两根为x1,x2,则下列表示正确的是( )A.x1+x2=3,x1x2=7B.x1+x2=-3,x1x2=7C.x1+x2=-3,x1x2=-7D.以上...
- 已知方程x2+(2k+1)x+k2-2=0的两实根的平方和等于11,k的取值是( )A.-3或1B.-3C.1D.3
- 先阅读,再回答问题:如果x1,x2是关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根,那么x1+x2,x1x2与系数a,b,c的关系是:x...
- 已知关于x的一元二次方程x2+x+m=0的一个实数根为1,那么它的另一个实数根是( )A.-2B.0C.1D.2
- 两根分别为-1和3,且二次项系数为1的一元二次方程是______.
- 关于x的方程2x2-(a2-4)x-a+1=0,(1)a为何值时,方程的一根为0?(2)a为何值时,两根互为相反数?(3)试证明:无论a取何...
- 已知:△ABC的两边AB、AC的长是关于x的一元二次方程x2-(2k+3)x+k2+3k+2=0的两个实数根,第三边BC的长为5.试问:k取何值时,...
- 已知a,b是方程x2+2x-5=0的两个根,则a2+b2+2a+2b-3=( )A.0B.1C.-1D.7
- 已知关于x的方程14x2-(m-2)x+m2=0(1)若方程有两个相等的实数根,求m的值,并求出此时方程的根;(2)是否存在正数m,使方程...