本试题 “已知圆锥的侧面积为12π.（1）求圆锥的母线l关于底面半径r的函数关系式，并求出r的取值范围；（2）当圆锥的全面积为16π时， 求圆锥的侧面展开图的圆心角度数.” 主要考查您对求反比例函数的解析式及反比例函数的应用
圆锥的计算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 求反比例函数的解析式及反比例函数的应用
- 圆锥的计算
反比例函数解析式的确定方法：
由于在反比例函数关系式 ：y=
中，只有一个待定系数k，确定了k的值，也就确定了反比例函数。因此，只需给出一组x、y的对应值或图象上一点的坐标，代入中即可求出k的值，从而确定反比例函数的关系式。但在实际求反比例函数的解析式时，应该具体问题具体分析。
反比例函数的应用：
建立函数模型，解决实际问题。
用待定系数法求反比例函数关系式的一般步骤是：
①设所求的反比例函数为：y=
(k≠0)；②根据已知条件（自变量与函数的对应值）列出含k的方程；
③由代人法解待定系数k的值；
④把k值代人函数关系式y=
中。反比例函数应用一般步骤：
①审题；
②求出反比例函数的关系式；
③求出问题的答案，作答。
圆锥：
以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转形成的面所围成的东西叫做圆锥体。该直角边叫圆锥的轴。
圆锥的组成构件：
①圆锥的高：圆锥的顶点到圆锥的底面圆心之间的距离叫做圆锥的高；
②圆锥的母线：圆锥的侧面展开形成的扇形的半径、底面圆周上点到顶点的距离。
③圆锥的侧面积：将圆锥的侧面沿母线展开，是一个扇形,这个扇形的弧长等于圆锥底面的周长,而扇形的半径等于圆锥的母线的长。
圆锥的侧面积就是弧长为圆锥底面的周长×母线/2；没展开时是一个曲面。
④圆锥有一个底面、一个侧面、一个顶点、一条高、无数条母线，且底面展开图为一圆形侧面展开图是扇形。
⑤圆锥侧面展开是一个扇形，已知扇形面积为二分之一rl。所以圆锥侧面积为二分之一母线长×弧长（即底面周长）。
另外，母线长等于底面圆直径的圆锥，展开的扇形就是半圆。
所有圆锥展开的扇形角度等于（底面直径÷母线）×180度。
圆锥的计算：
设圆锥底面圆的半径为r，母线长为l，n为圆心角度数
则圆锥的侧面积：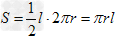
，
圆锥的全面积：S=S侧+S底=
，
圆锥的体积：V=
Sh=·πr2h
底面周长（C）=2πr=（nπl）/
h=根号（l2-r2）
发现相似题
与“已知圆锥的侧面积为12π.（1）求圆锥的母线l关于底面半径r的函...”考查相似的试题有：
- 请你写出一个图象在第二、四象限的反比例函数 ．
- 对于反比例函数,下列说法不正确的是（ ）A．它的图象是双曲线并且在第一、三象限B．点（-4,）在它的图象上C．它的图象是中心...
- 某长方体的体积为100cm3，长方体的高h（单位：cm）与底面积S的函数关系式为（ ）A.h=B.h= C．h=100S D．h=100
- 函数y=kx（k＞0）的图象上两点A（x1，y1）和B（x2，y2），且x1＞x2＞0，分别过A，B向x轴作AA1⊥x轴于A1，BB1⊥x轴于B1，则S△AA1...
- 已知y=y1-y2，y1与x+2成正比例，y2与x成反比例，且当x=1时，y=0；当x=4时，y=7．（1）求x与y的函数关系；（2）求x=2时，y的值．
- 已知(x1，y1)，(x2，y2)，(x3，y3)是反比例函数的图象上的三点，且x1＜x2＜0，x3＞0，则y1，y2，y3的大小关系是( )．A．y3＜y...
- 已知圆柱的底面半径为1，母线长为2，则圆柱的侧面积为[ ]A.2B.4C.D.
- 如图，小明想用图中所示的扇形纸片围成一个圆锥，已知扇形的半径为5cm，弧长是6πcm，那么围成的圆锥的高度是（ ）cm。
- 如图，已知圆锥的母线AC=6cm，侧面展开图是半圆，则底面半径OC=______．
- 用一块圆心角为150°，面积为240πcm2的扇形硬纸片围成一个圆锥模型（相交粘贴部分忽略不计）．求圆锥模型的底面半径．