正比例：
两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量相对应的两个数的比值（也就是商）一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系，正比例的图像是一条直线；
用字母表示为如果用字母x和y表示两种相关联的量，用k表示它们的比值（一定），正比例关系可以用以下关系式表示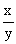：=k（一定）；
正比例关系两种相关联的量的变化规律：同时扩大，同时缩小，比值不变．正比例和反比例

反比例：
两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系叫做反比例关系；
如果用字母x和y表示两种相关联的量，用k表示它们的积，反比例关系可以用下面关系式表示：xy=k（一定）。

正比例和反比例关系：
相同点：
①正比例和反比例都含有三个数量，在这三个数量中，均有一个定量、两个变量。
②在正、反比例的两个变量中，均是一个量变化，另一个量也随之变化。并且变化方式均属于扩大（乘以一个数）或缩小（除以一个数）若干倍的变化。
不同点：
①正比例的定量是两个变量中相对应的两个数的比值。反比例的定量是两个变量中相对应的两个数的积。
②正比例的图像时上升直线；反比例是曲线。
③公式不同：正比例是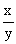（=k（一定）），反比例是（xy=k（一定））。
④规律不同：正比例是一个数缩小，另一个数也缩小，一个数扩大，另一个数也扩大；反比例是一个数缩小，另一个数就扩大，一个数扩大另一个数就缩小。　

比例尺分类：
比例尺一般分为数值比例尺和线段比例尺：
（1）数值比例尺：例如一幅图的比例尺是1：20000或。为了方便，通常把比例尺写成前项（或后项）是1的比。
（2）线段比例尺是在图上附上一条标有数量的线段，用来表示实际相对应的距离。

比例尺表示方法：
用公式表示为：比例尺=。比例尺通常有三种表示方法。
①数字式，用数字的比例式或分数式表示比例尺的大小。例如地图上1厘米代表实地距离500千米，可写成：1∶50,000,000或写成：1/50,000,000。
②线段式，在地图上画一条线段，并注明地图上1厘米所代表的实际距离。
③文字式，在地图上用文字直接写出地图上1厘米代表实地距离多少千米，如：图上1厘米相当于地面距离500千米，或五千万分之一。
三种表示方法可以互换。必须化单位。
在绘制地图和其他平面图的时候，需要把实际距离按一定的比缩小（或扩大），再画在图纸上。
这时，就要确定图上距离和相对应的实际距离的比。

比例尺公式：
图上距离=实际距离×比例尺　
实际距离=图上距离÷比例尺　
比例尺=图上距离÷实际距离

单位换算：
在比例尺计算中要注意单位间的换算：1公里=1千米=1×1000米=1×100000厘米
图上用厘米，实地用千米，厘米换千米，去五个零；
千米换厘米，在千的基础上再加两个零。

计算方法：
①如果将原比例尺放大到n倍;那么原比例×n。
②如果将原比例尺放大n倍;那么原比例×(n+1)。
③如果将原比例尺缩小到1/n;那么原比例×1/n。
④如果将原比例尺缩小1/n;那么原比例×(1-1/n)。
⑤比例尺缩放后,原面积之比会变为缩放倍数的平方。