本试题 “设圆C的圆心在双曲线(a>0)的右焦点且与此双曲线的渐近线相切,若圆C被直线l:截得的弦长等于2,则a=( )” 主要考查您对直线与圆的位置关系
双曲线的性质(顶点、范围、对称性、离心率)
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 直线与圆的位置关系
- 双曲线的性质(顶点、范围、对称性、离心率)
直线与圆的位置关系:
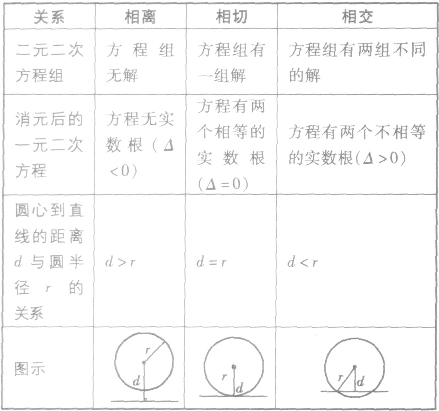
由直线与圆的公共点的个数,得出以下直线和圆的三种位置关系:
(1)相交:直线与圆有两个公共点时,叫做直线和圆相交,这时直线叫做圆的割线。
(2)相切:直线和圆有唯一公共点时,叫做直线和圆相切,这时直线叫做圆的切线,唯一的公共点叫做切点。
(3)相离:直线和圆没有公共点时,叫做直线和圆相离。
其图像如下: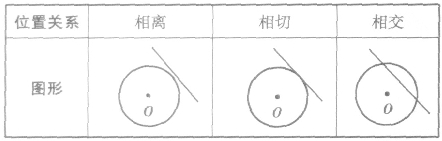
直线和圆的位置关系的性质:
(1)直线l和⊙O相交 d<r
d<r
(2)直线l和⊙O相切 d=r;
d=r;
(3)直线l和⊙O相离 d>r。
d>r。
直线与圆位置关系的判定方法:
(1)代数法:判断直线Ax+By+C=0和圆x2+y2+Dx+Ey+F=0的位置关系,可由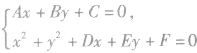
推出mx2+nx+p=0,利用判别式△进行判断.
△>0则直线与圆相交;
△=0则直线与圆相切;
△<0则直线与圆相离.
(2)几何法:已知直线Ax+By+C=0和圆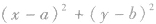
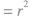 ,圆心到直线的距离
,圆心到直线的距离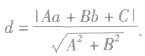
d<r则直线和圆相交;
d=r则直线和圆相切;
d>r则直线和圆相离.
特别提醒:
(1)上述两种方法,以利用圆心到直线的距离进行判定较为简捷,而判别式法也适用于直线与椭圆、双曲线、抛物线位置关系的判断.
(2)直线与圆相交,应抓住半径、弦心距、半弦长组成的直角三角形,可使解法简单.
直线与圆位置关系的判定方法列表如下:
直线与圆相交的弦长公式:
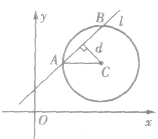
(1)几何法:如图所示,直线l与圆C相交于A、B两点,线段AB的长即为l与圆相交的弦长。
设弦心距为d,半径为r,弦为AB,则有|AB|=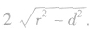
(2)代数法:直线l与圆交于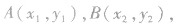 直线l的斜率为k,则有
直线l的斜率为k,则有
当直线AB的倾斜角为直角,即斜率不存在时,|AB|=
双曲线的离心率的定义:
(1)定义:双曲线的焦距与实轴长的比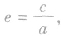 叫做双曲线的离心率.
叫做双曲线的离心率.
(2)e的范围:e>l.
(3)e的含义:e是表示双曲线开口大小的一个量,e越大开口越大.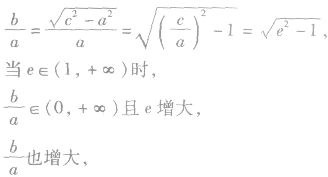
渐近线与实轴的夹角也增大。
双曲线的性质:
1、焦点在x轴上:顶点:(a,0),(-a,0);焦点:(c,0),(-c,0);
渐近线方程: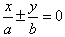 或
或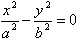 。
。
2、焦点在y轴上:顶点:(0,-a),(0,a);焦点:(0,c),(0,-c);
渐近线方程: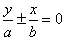 或
或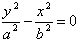 。
。
3、轴:x、y为对称轴,实轴长为2a,虚轴长为2b,焦距2c。
4、离心率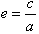 ;
;
5、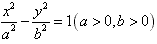 中,取值范围:x≤-a或x≥a,y∈R,对称轴是坐标轴,对称中心是原点。
中,取值范围:x≤-a或x≥a,y∈R,对称轴是坐标轴,对称中心是原点。
双曲线的焦半径:
双曲线上的点 之间的线段长度称作焦半径,分别记作
之间的线段长度称作焦半径,分别记作

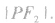
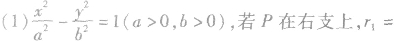
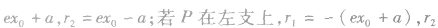
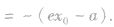
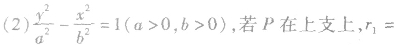
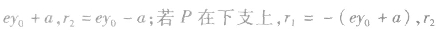

(2)焦点三角形:已知
 的两个焦点,P为双曲线上一点(异于顶点),
的两个焦点,P为双曲线上一点(异于顶点),
 的面积为
的面积为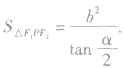
在解决与焦点三角形有关的问题时,应注意双曲线的两个定义、焦半径公式以及三角形的边角关系、正弦定理等知识的综合运用,还应注意灵活地运用平面几何、三角函数等知识来分析解决问题.
(3)基础三角形:如图所示,△AOB中,

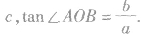
(5)自双曲线的焦点作渐近线的垂线,垂足必在相应的准线上,即过焦点所作的渐近线的垂线,渐近线及相应准线三线共点.
(6)以双曲线的焦半径为直径的圆与以实轴为直径的圆外切或内切.
(7)双曲线
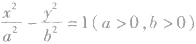 上一点P(x0,y0)处的切线方程是
上一点P(x0,y0)处的切线方程是
(8)双曲线划分平面区域:对于双曲线
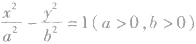 ,我们有:P(x0,y0)在双曲线内部(与焦点共区域)
,我们有:P(x0,y0)在双曲线内部(与焦点共区域)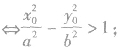 P(x0,y0)在双曲线外部(与焦点不其区域)
P(x0,y0)在双曲线外部(与焦点不其区域)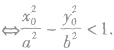
与“设圆C的圆心在双曲线(a>0)的右焦点且与此双曲线的渐近线相...”考查相似的试题有:
- 给定点A(x0,y0),圆C:x2+y2=r2及直线l:x0x+y0y=r2,给出以下三个命题:①当点A在圆C上时,直线l与圆C相切;②当点A在圆C内...
- 已知以椭圆x2a2+y2b2=1(a>b>0)的右焦点F为圆心,a为半径的圆与直线l:x=a2c(其中c=a2-b2)交于不同的两点,则该椭圆的离心...
- 过点P(2,3)向圆x2+y2=1作两条切线PA、PB,则弦AB所在直线的方程为( )A.2x-3y-1=0B.2x+3y-1=0C.3x+2y-1=0D.3x-2y-1=0
- 直线3x-4y+3=0被圆x2+y2=1所截截得的弦长为( )A.45B.85C.2D.3
- 若关于的方程有且只有两个不同的实数根,则实数的取值范围是[ ]A.B.C.D.
- 已知双曲线C:x2a2-y2b2=1(a>0,b>0)的离心率为52,则C的渐近线方程为( )A.y=±14xB.y=±13xC.y=±xD.y=±12x
- 若双曲线x2-y2=1右支上一点A(a,b)到直线y=x的距离为2,则a+b=______.
- 过双曲线x2a2-y2b2=1(b>a>0)的左焦点F(-c,0)(c>0)作圆x2+y2=a2的切线,切点为E,延长FE交双曲线右支于点P,若OE=12(O...
- 设双曲线x2m+y2n=1的离心率为2,且一个焦点与抛物线x2=8y的焦点相同,则此双曲线的方程为______.
- 下列曲线中离心率为的是[ ]A、B、C、D、