本试题 “如图,∠ACB=∠CDB=60°,则△ABC是______三角形.” 主要考查您对等边三角形
圆心角,圆周角,弧和弦
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 等边三角形
- 圆心角,圆周角,弧和弦
三条边都相等的三角形叫做等边三角形,“等边三角形”也被称为“正三角形”。是特殊的等腰三角形。
如果一个三角形满足下列任意一条,则它必满足另一条,三边相等或三角相等的三角形叫做等边三角形:
1.三边长度相等;
2.三个内角度数均为60度;
3.一个内角为60度的等腰三角形。
性质:
①等边三角形是锐角三角形,等边三角形的内角都相等,且均为60°。
②等边三角形每条边上的中线、高线和所对角的平分线互相重合(三线合一)
③等边三角形是轴对称图形,它有三条对称轴,对称轴是每条边上的中线、高线 或对角的平分线所在的直线。
④等边三角形重心、内心、外心、垂心重合于一点,称为等边三角形的中心。(四心合一)
⑤等边三角形内任意一点到三边的距离之和为定值(等于其高)
判定方法:
①三边相等的三角形是等边三角形(定义)
②三个内角都相等(为60度)的三角形是等边三角形
③有一个角是60度的等腰三角形是等边三角形
④ 两个内角为60度的三角形是等边三角形
说明:可首先考虑判断三角形是等腰三角形。
等边三角形的性质与判定理解:
首先,明确等边三角形定义。三边相等的三角形叫做等边三角形,也称正三角形。
其次,明确等边三角形与等腰三角形的关系。等边三角形是特殊的等腰三角形,等腰三角形不一定是等边三角形。
等比三角形的尺规做法:
可以利用尺规作图的方式画出正三角形,其作法相当简单:先用尺画出一条任意长度的线段(这条线段的长度决定等边三角形的边长),再分别以线段二端点为圆心、线段为半径画圆,二圆汇交于二点,任选一点,和原来线段的两个端点画线段,则这二条线段和原来线段即构成一正三角形。
圆的定义:
在同一平面内,到定点的距离等于定长的点的集合叫做圆。这个定点叫做圆的圆心。图形一周的长度,就是圆的周长。
弧:
圆上任意两点间的部分叫做圆弧,简称弧。
弧用符号“⌒”表示以A,B为端点的弧记作“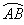 ”,读作“圆弧AB”或“弧AB”。
”,读作“圆弧AB”或“弧AB”。
优弧:大于半圆的弧(多用三个字母表示);
劣弧:小于半圆的弧(多用两个字母表示)
圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆。
弧、弦、弦心距、圆心角之间的关系定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等。
推论:在同圆或等圆中,如果两个圆的圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。
圆心角:
顶点在圆心的角叫做圆心角。
圆周角:
顶点在圆上,并且两边都和圆相交的角叫做圆周角。
圆周角的顶点在圆上,它的两边为圆的两条弦。
圆心角特征识别:
①顶点是圆心;
②两条边都与圆周相交。
计算公式:
①L(弧长)=n/180Xπr(n为圆心角度数,以下同);
②S(扇形面积) = n/360Xπr2;
③扇形圆心角n=(180L)/(πr)(度)。
④K=2Rsin(n/2) K=弦长;n=弦所对的圆心角,以度计。
圆心角定理:
圆心角的度数等于它所对的弧的度数。
理解:(定义)
(1)等弧对等圆心角
(2)把顶点在圆心的周角等分成360份时,每一份的圆心角是1°的角.
(3)因为在同圆中相等的圆心角所对的弧相等,所以整个圆也被等分成360份,这时,把每一份这样得到的弧叫做1°的弧.
(4)圆心角的度数和它们对的弧的度数相等.
推论:
在同圆或等圆中,如果(1)两个圆心角,(2)两条弧,(3)两条弦(4)两条弦上的弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等
与圆周角关系:
在同圆或等圆中,同弧或同弦所对的圆周角等于二分之一的圆心角。
定理证明:分三种情况讨论,始终做直径COD,利用等腰三角形等腰底角相等,外角等于两内角之和来证明。
圆周角定理推论:
圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角都等于这条弧所对的圆心角的一半。
①圆周角度数定理:圆周角的度数等于它所对的弧的度数的一半。
②同圆或等圆中,圆周角等于它所对的弧上的圆心角的一半。
③同圆或等圆中,同弧或等弧所对的圆周角相等,相等圆周角所对的弧也相等。(不在同圆或等圆中其实也相等的。注:仅限这一条。)
④半圆(或直径)所对圆周角是直角,90°的圆周角所对的弦是直径。
⑤圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
⑥在同圆或等圆中,圆周角相等<=>弧相等<=>弦相等。
与“如图,∠ACB=∠CDB=60°,则△ABC是______三角形.”考查相似的试题有:
- 如图,已知△ABC中,∠C=90°,∠B=60°,AC=4,等边△DEF的一边在直角边AC上移动,当点E与点C重合时,点D恰好落在AB边上,(1)求...
- 有一角为60°的等腰三角形是______.
- 已知:如图,点O2是⊙O1上一点,⊙O2与⊙O1相交于A、D两点,BC⊥AD,垂足为D,分别交⊙O1、⊙O2于B、C两点,延长DO2交⊙O2于E,交BA...
- 如图,已知BD是⊙O的直径,点A、C在⊙O上,AB=BC,∠AOB=60°,则∠BDC的度数是( )A.20°B.25°C.30°D.40°
- 如图,点B、C在⊙O上,且∠OBC=60°,则圆周角∠BAC等于( )A.60°B.50°C.40°D.30°
- 如图,在⊙O中,AB=2CD,那么( )A.AB>2CDB.AB<2CDC.AB=2CDD.AB与2CD的大小关系无法比较
- 如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA、OB在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆...
- 如图,正方形ABCD是⊙O的内接正方形,点P在劣弧上不同于点C得到任意一点,则∠BPC的度数是( )A.45°B.60°C.75°D.90°
- 如图所示,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折...
- 如图,过⊙O的直径AB上两点M,N,分别作弦CD,EF,若CD∥EF,AC=BF.求证:(1)弧BEC=弧ADF;(2)AM=BN.