本试题 “如图,抛物线y=x2﹣2x﹣3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.(1)求A、B两点的坐标及直线AC的函数表达式;...” 主要考查您对一次函数的图像
求一次函数的解析式及一次函数的应用
二次函数的图像
求二次函数的解析式及二次函数的应用
平行四边形的性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 一次函数的图像
- 求一次函数的解析式及一次函数的应用
- 二次函数的图像
- 求二次函数的解析式及二次函数的应用
- 平行四边形的性质
函数不是数,它是指某一变化过程中两个变量之间的关系
一次函数的图象:一条直线,过(0,b),(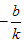 ,0)两点。
,0)两点。
性质:
(1)在一次函数图像上的任取一点P(x,y),则都满足等式:y=kx+b(k≠0)。
(2)一次函数与y轴交点的坐标总是(0,b),与x轴总交于(-b/k,0)。正比例函数的图像都经过原点。
k,b决定函数图像的位置:
y=kx时,y与x成正比例:
当k>0时,直线必通过第一、三象限,y随x的增大而增大;
当k<0时,直线必通过第二、四象限,y随x的增大而减小。
y=kx+b时:
当 k>0,b>0, 这时此函数的图象经过第一、二、三象限;
当 k>0,b<0,这时此函数的图象经过第一、三、四象限;
当 k<0,b>0,这时此函数的图象经过第一、二、四象限;
当 k<0,b<0,这时此函数的图象经过第二、三、四象限。
当b>0时,直线必通过第一、二象限;
当b<0时,直线必通过第三、四象限。
特别地,当b=0时,直线经过原点O(0,0)。
这时,当k>0时,直线只通过第一、三象限,不会通过第二、四象限。
当k<0时,直线只通过第二、四象限,不会通过第一、三象限。
特殊位置关系:
当平面直角坐标系中两直线平行时,其函数解析式中k的值(即一次项系数)相等;
当平面直角坐标系中两直线垂直时,其函数解析式中k的值互为负倒数(即两个k值的乘积为-1)一次函数的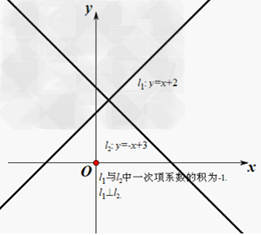
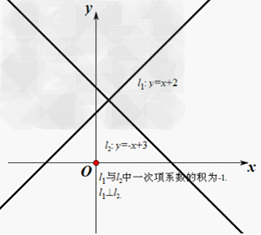
画法:
(1)列表:表中给出一些自变量的值及其对应的函数值。
(2)描点:在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点。
一般地,y=kx+b(k≠0)的图象过(0,b)和(-b/k,0)两点即可画出。
正比例函数y=kx(k≠0)的图象是过坐标原点的一条直线,一般取(0,0)和(1,k)两点画出即可。
(3)连线: 按照横坐标由小到大的顺序把描出的各点用直线连接起来。
先设出函数解析式,再根据条件确定解析式中的未知系数,从而得到函数的解析式的方法。
一次函数的应用:
应用一次函数解应用题,一般是先写出函数解析式,在依照题意,设法求解。
(1)有图像的,注意坐标轴表示的实际意义及单位;
(2)注意自变量的取值范围。
用待定系数法求一次函数解析式的四个步骤:
第一步(设):设出函数的一般形式。(称一次函数通式)
第二步(代):代入解析式得出方程或方程组。
第三步(求):通过列方程或方程组求出待定系数k,b的值。
第四步(写):写出该函数的解析式。
一次函数的应用涉及问题:
一、分段函数问题
分段函数是在不同区间有不同对应方式的函数,要特别注意自变量取值范围的划分,既要科学合理,又要符
合实际。
二、函数的多变量问题
解决含有多变量问题时,可以分析这些变量的关系,选取其中一个变量作为自变量,然后根据问题的条件寻
求可以反映实际问题的函数
三、概括整合
(1)简单的一次函数问题:①建立函数模型的方法;②分段函数思想的应用。
(2)理清题意是采用分段函数解决问题的关键。
生活中的应用:
1.当时间t一定,距离s是速度v的一次函数。s=vt。
2.如果水池抽水速度f一定,水池里水量g是抽水时间t的一次函数。设水池中原有水量S。g=S-ft。
3.当弹簧原长度b(未挂重物时的长度)一定时,弹簧挂重物后的长度y是重物重量x的一次函数,即y=kx+b(k为任意正数)
一次函数应用常用公式:
1.求函数图像的k值:(y1-y2)/(x1-x2)
2.求与x轴平行线段的中点:(x1+x2)/2
3.求与y轴平行线段的中点:(y1+y2)/2
4.求任意线段的长:√[(x1-x2)2+(y1-y2)2 ]
5.求两个一次函数式图像交点坐标:解两函数式
两个一次函数 y1=k1x+b1; y2=k2x+b2 令y1=y2 得k1x+b1=k2x+b2 将解得的x=x0值代回y1=k1x+b1 ; y2=k2x+b2 两式任一式 得到y=y0 则(x0,y0)即为 y1=k1x+b1 与 y2=k2x+b2 交点坐标
6.求任意2点所连线段的中点坐标:[(x1+x2)/2,(y1+y2)/2]
7.求任意2点的连线的一次函数解析式:(x-x1)/(x1-x2)=(y-y1)/(y1-y2) (若分母为0,则分子为0)
(x,y)为 + ,+(正,正)时该点在第一象限
(x,y)为 - ,+(负,正)时该点在第二象限
(x,y)为 - ,-(负,负)时该点在第三象限
(x,y)为 + ,-(正,负)时该点在第四象限
8.若两条直线y1=k1x+b1//y2=k2x+b2,则k1=k2,b1≠b2
9.如两条直线y1=k1x+b1⊥y2=k2x+b2,则k1×k2=-1
10.
y=k(x-n)+b就是直线向右平移n个单位
y=k(x+n)+b就是直线向左平移n个单位
y=kx+b+n就是向上平移n个单位
y=kx+b-n就是向下平移n个单位
口决:左加右减相对于x,上加下减相对于b。
11.直线y=kx+b与x轴的交点:(-b/k,0) 与y轴的交点:(0,b)
是一条关于
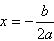 对称的曲线,这条曲线叫抛物线。
对称的曲线,这条曲线叫抛物线。 抛物线的主要特征:
①有开口方向,a表示开口方向:a>0时,抛物线开口向上;a<0时,抛物线开口向下;
②有对称轴;
③有顶点;
④c 表示抛物线与y轴的交点坐标:(0,c)。
二次函数图像性质:
轴对称:
二次函数图像是轴对称图形。对称轴为直线x=-b/2a
对称轴与二次函数图像唯一的交点为二次函数图像的顶点P。
特别地,当b=0时,二次函数图像的对称轴是y轴(即直线x=0)。
a,b同号,对称轴在y轴左侧
b=0,对称轴是y轴
a,b异号,对称轴在y轴右侧
顶点:
二次函数图像有一个顶点P,坐标为P ( h,k )
当h=0时,P在y轴上;当k=0时,P在x轴上。即可表示为顶点式y=a(x-h)^2+k。
h=-b/2a, k=(4ac-b^2)/4a。
开口:
二次项系数a决定二次函数图像的开口方向和大小。
当a>0时,二次函数图像向上开口;当a<0时,抛物线向下开口。
|a|越大,则二次函数图像的开口越小。
决定对称轴位置的因素:
一次项系数b和二次项系数a共同决定对称轴的位置。
当a>0,与b同号时(即ab>0),对称轴在y轴左; 因为对称轴在左边则对称轴小于0,也就是- b/2a<0,所以 b/2a要大于0,所以a、b要同号
当a>0,与b异号时(即ab<0),对称轴在y轴右。因为对称轴在右边则对称轴要大于0,也就是- b/2a>0, 所以b/2a要小于0,所以a、b要异号
可简单记忆为左同右异,即当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时(即ab<0 ),对称轴在y轴右。
事实上,b有其自身的几何意义:二次函数图像与y轴的交点处的该二次函数图像切线的函数解析式(一次函数)的斜率k的值。可通过对二次函数求导得到。
决定与y轴交点的因素:
常数项c决定二次函数图像与y轴交点。
二次函数图像与y轴交于(0,C)
注意:顶点坐标为(h,k), 与y轴交于(0,C)。
与x轴交点个数:
a<0;k>0或a>0;k<0时,二次函数图像与x轴有2个交点。
k=0时,二次函数图像与x轴只有1个交点。
a<0;k<0或a>0,k>0时,二次函数图像与X轴无交点。
当a>0时,函数在x=h处取得最小值ymin=k,在x<h范围内是减函数,在x>h范围内是增函数(即y随x的变大而变小),二次函数图像的开口向上,函数的值域是y>k
当a<0时,函数在x=h处取得最大值ymax=k,在x<h范围内是增函数,在x>h范围内是减函数(即y随x的变大而变大),二次函数图像的开口向下,函数的值域是y<k
当h=0时,抛物线的对称轴是y轴,这时,函数是偶函数。
最常用的方法是待定系数法,根据题目的特点,选择恰当的形式,一般,有如下几种情况:
(1)已知抛物线上三点的坐标,一般选用一般式;
(2)已知抛物线顶点或对称轴或最大(小)值,一般选用顶点式;
(3)已知抛物线与x轴的两个交点的横坐标,一般选用两点式;
(4)已知抛物线上纵坐标相同的两点,常选用顶点式。
二次函数的应用:
(1)应用二次函数才解决实际问题的一般思路:
理解题意;
建立数学模型;
解决题目提出的问题。
(2)应用二次函数求实际问题中的最值:
即解二次函数最值应用题,设法把关于最值的实际问题转化为二次函数的最值问题,然后按求二次函数最值的方法求解。
求最值时,要注意求得答案要符合实际问题。
二次函数的三种表达形式:
①一般式:
y=ax2+bx+c(a≠0,a、b、c为常数),顶点坐标为 [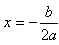 ,
,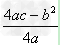 ]
]
把三个点代入函数解析式得出一个三元一次方程组,就能解出a、b、c的值。
②顶点式:
y=a(x-h)2+k(a≠0,a、h、k为常数),顶点坐标为对称轴为直线x=h,顶点的位置特征和图像的开口方向与函数y=ax2的图像相同,当x=h时,y最值=k。
有时题目会指出让你用配方法把一般式化成顶点式。
例:已知二次函数y的顶点(1,2)和另一任意点(3,10),求y的解析式。
解:设y=a(x-1)2+2,把(3,10)代入上式,解得y=2(x-1)2+2。
注意:与点在平面直角坐标系中的平移不同,二次函数平移后的顶点式中,h>0时,h越大,图像的对称轴离y轴越远,且在x轴正方向上,不能因h前是负号就简单地认为是向左平移。
具体可分为下面几种情况:
当h>0时,y=a(x-h)2的图象可由抛物线y=ax2向右平行移动h个单位得到;
当h<0时,y=a(x-h)2的图象可由抛物线y=ax2向左平行移动|h|个单位得到;
当h>0,k>0时,将抛物线y=ax2向右平行移动h个单位,再向上移动k个单位,就可以得到y=a(x-h)2+k的图象;
当h>0,k<0时,将抛物线y=ax2向右平行移动h个单位,再向下移动|k|个单位可得到y=a(x-h)2+k的图象;
当h<0,k>0时,将抛物线y=ax2向左平行移动|h|个单位,再向上移动k个单位可得到y=a(x-h)2+k的图象;
当h<0,k<0时,将抛物线y=ax2向左平行移动|h|个单位,再向下移动|k|个单位可得到y=a(x-h)2+k的图象。
③交点式:
y=a(x-x1)(x-x2) (a≠0) [仅限于与x轴即y=0有交点时的抛物线,即b2-4ac≥0] .
已知抛物线与x轴即y=0有交点A(x1,0)和 B(x2,0),我们可设y=a(x-x1)(x-x2),然后把第三点代入x、y中便可求出a。
由一般式变为交点式的步骤:
二次函数
∵x1+x2=-b/a, x1?x2=c/a(由韦达定理得),
∴y=ax2+bx+c
=a(x2+b/ax+c/a)
=a[x2-(x1+x2)x+x1?x2]
=a(x-x1)(x-x2).
重要概念:
a,b,c为常数,a≠0,且a决定函数的开口方向。a>0时,开口方向向上;
a<0时,开口方向向下。a的绝对值可以决定开口大小。
a的绝对值越大开口就越小,a的绝对值越小开口就越大。
能灵活运用这三种方式求二次函数的解析式;
能熟练地运用二次函数在几何领域中的应用;
能熟练地运用二次函数解决实际问题。
二次函数的其他表达形式:
①牛顿插值公式:
f(x)=f[x0]+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x-x1)+...f[x0,...xn](x-x0)...(x-xn-1)+Rn(x)由此可引导出交点式的系数a=y/(x·x)(y为截距)
二次函数表达式的右边通常为二次三项式。
双根式
y=a(x-x1)*(x-x2)
若ax2+bx+c=0有两个实根x1,x2,则y=a(x-x1)(x-x2)此抛物线的对称轴为直线x=(x1+x2)/2。
③三点式
已知二次函数上三个点,(x1,f(x1))(x2,f(x2))(x3,f(x3))
则f(x)=f(x3)(x-x1)(x-x2)/(x3-x1)(x3-x2)+f(x2)(x-x1)*(x-x3)/(x2-x1)(x2-x3)+f(x1)(x-x2)(x-x3)/(x1-x2)(x1-x3)
与X轴交点的情况
当△=b2-4ac>0时,函数图像与x轴有两个交点。(x1,0), (x2,0);
当△=b2-4ac=0时,函数图像与x轴只有一个交点。(-b/2a,0)。
Δ=b2-4ac<0时,抛物线与x轴没有交点。
X的取值是虚数(x=-b±√b2-4ac的值的相反数,乘上虚数i,整个式子除以2a)
二次函数解释式的求法:
就一般式y=ax2+bx+c(其中a,b,c为常数,且a≠0)而言,其中含有三个待定的系数a ,b ,c.求二次函数的一般式时,必须要有三个独立的定量条件,来建立关于a ,b ,c 的方程,联立求解,再把求出的a ,b ,c 的值反代回原函数解析式,即可得到所求的二次函数解析式。
1.巧取交点式法:
知识归纳:二次函数交点式:y=a(x-x1)(x-x2) (a≠0)x1,x2分别是抛物线与x轴两个交点的横坐标。
已知抛物线与x轴两个交点的横坐标求二次函数解析式时,用交点式比较简便。
①典型例题一:告诉抛物线与x轴的两个交点的横坐标,和第三个点,可求出函数的交点式。
例:已知抛物线与x轴交点的横坐标为-2和1 ,且通过点(2,8),求二次函数的解析式。
点拨:
解设函数的解析式为y=a(x+2)(x-1),
∵过点(2,8),
∴8=a(2+2)(2-1)。
解得a=2,
∴抛物线的解析式为:
y=2(x+2)(x-1),
即y=2x2+2x-4。
②典型例题二:告诉抛物线与x轴的两个交点之间的距离和对称轴,可利用抛物线的对称性求解。
例:已知二次函数的顶点坐标为(3,-2),并且图象与x轴两交点间的距离为4,求二次函数的解析式。
点拨:
在已知抛物线与x轴两交点的距离和顶点坐标的情况下,问题比较容易解决.由顶点坐标为(3,-2)的条件,易知其对称轴为x=3,再利用抛物线的对称性,可知图象与x轴两交点的坐标分别为(1,0)和(5,0)。此时,可使用二次函数的交点式,得出函数解析式。
2.巧用顶点式:
顶点式y=a(x-h)2+k(a≠0),其中(h,k)是抛物线的顶点。当已知抛物线顶点坐标或对称轴,或能够先求出抛物线顶点时,设顶点式解题十分简洁,因为其中只有一个未知数a。在此类问题中,常和对称轴,最大值或最小值结合起来命题。在应用题中,涉及到桥拱、隧道、弹道曲线、投篮等问题时,一般用顶点式方便.
①典型例题一:告诉顶点坐标和另一个点的坐标,直接可以解出函数顶点式。
例:已知抛物线的顶点坐标为(-1,-2),且通过点(1,10),求此二次函数的解析式。
点拨:
解∵顶点坐标为(-1,-2),
故设二次函数解析式为y=a(x+1)2-2 (a≠0)。
把点(1,10)代入上式,得10=a·(1+1)2-2。
∴a=3。
∴二次函数的解析式为y=3(x+1)2-2,即y=3x2+6x+1。
②典型例题二:
如果a>0,那么当  时,y有最小值且y最小=
时,y有最小值且y最小= ;
;
如果a<0,那么,当 时,y有最大值,且y最大=
时,y有最大值,且y最大= 。
。
告诉最大值或最小值,实际上也是告诉了顶点坐标,同样也可以求出顶点式。
例:已知二次函数当x=4时有最小值-3,且它的图象与x轴两交点间的距离为6,求这个二次函数的解析式。
点拨:
析解∵二次函数当x=4时有最小值-3,∴顶点坐标为(4,-3),对称轴为直线x=4,抛物线开口向上。
由于图象与x轴两交点间的距离为6,根据图象的对称性就可以得到图象与x轴两交点的坐标是(1,0)和(7,0)。
∴抛物线的顶点为(4,-3)且过点(1,0)。
故可设函数解析式为y=a(x-4)2-3。
将(1,0)代入得0=a(1-4)2-3, 解得a=13.
∴y=13(x-4)2-3,即y=13x2-83x+73。
③典型例题三:告诉对称轴,相当于告诉了顶点的横坐标,综合其他条件,也可解出。
例如:
(1)已知二次函数的图象经过点A(3,-2)和B(1,0),且对称轴是直线x=3.求这个二次函数的解析式.
(2)已知关于x的二次函数图象的对称轴是直线x=1,图象交y轴于点(0,2),且过点(-1,0),求这个二次函数的解析式.
(3)已知抛物线的对称轴为直线x=2,且通过点(1,4)和点(5,0),求此抛物线的解析式.
(4)二次函数的图象的对称轴x=-4,且过原点,它的顶点到x轴的距离为4,求此函数的解析式.
④典型例题四:利用函数的顶点式,解图像的平移等问题非常方便。
例:把抛物线y=ax2+bx+c的图像向右平移3 个单位, 再向下平移2 个单位, 所得图像的解析式是y=x2-3x+5, 则函数的解析式为_______。
点拨:
解先将y=x2-3x+5化为y=(x-32)2+5-94, 即y=(x-32)2+114。
∵它是由抛物线的图像向右平移3 个单位, 再向下平移2 个单位得到的,
∴原抛物线的解析式是y=(x-32+3)2+114+2=(x+32)2+194=x2+3x+7。
两组对边分别平行的四边形叫做平行四边形。
平行四边形用符号“□ABCD,如平行四边形ABCD记作“□ABCD”,读作ABCD”。
①平行四边形属于平面图形。
②平行四边形属于四边形。
③平行四边形中还包括特殊的平行四边形:矩形,正方形和菱形等。
④平行四边形属于中心对称图形。
平行四边形的性质:
主要性质
(矩形、菱形、正方形都是特殊的平行四边形。)
(1)如果一个四边形是平行四边形,那么这个四边形的两组对边分别相等。
(简述为“平行四边形的两组对边分别相等”)
(2)如果一个四边形是平行四边形,那么这个四边形的两组对角分别相等。
(简述为“平行四边形的两组对角分别相等”)
(3)如果一个四边形是平行四边形,那么这个四边形的邻角互补
(简述为“平行四边形的邻角互补”)
(4)夹在两条平行线间的平行线段相等。
(5)如果一个四边形是平行四边形,那么这个四边形的两条对角线互相平分。
(简述为“平行四边形的对角线互相平分”)
(6)连接任意四边形各边的中点所得图形是平行四边形。(推论)
(7)平行四边形的面积等于底和高的积。(可视为矩形)
(8)过平行四边形对角线交点的直线,将平行四边形分成全等的两部分图形。
(9)平行四边形是中心对称图形,对称中心是两对角线的交点.
(10)平行四边形不是轴对称图形,矩形和菱形是轴对称图形。
注:正方形,矩形以及菱形也是一种特殊的平行四边形,三者具有平行四边形的性质。
(11)平行四边形ABCD中(如图)E为AB的中点,则AC和DE互相三等分,一般地,若E为AB上靠近A的n等分点,则AC和DE互相(n+1)等分。
(12)平行四边形ABCD中,AC、BD是平行四边形ABCD的对角线,则各四边的平方和等于对角线的平方和。
(13)平行四边形对角线把平行四边形面积分成四等分。
(14)平行四边形中,两条在不同对边上的高所组成的夹角,较小的角等于平行四边形中较小的角,较大的角等于平行四边形中较大的角。
(15)平行四边形中,一个角的顶点向他对角的两边所做的高,与这个角的两边组成的夹角相等。
与“如图,抛物线y=x2﹣2x﹣3与x轴交A、B两点(A点在B点左侧),...”考查相似的试题有:
- 在直角坐标系xOy中,直线l过(1,3)和(3,1)两点,且与x轴,y轴分别交于A,B两点.(1)求直线l的函数关系式;(2)求△AOB...
- 如图2,已知抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标为 (2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上...
- 在平面直角坐标系中,将抛物线先向右平移2个单位,再向上平移2个单位,得到的抛物线解析式为 ( )A.B.C.D.
- 函数y=x2,当x=( )时,函数的值等于2。
- 设人民币定期储蓄的年利率是x,一年到期后,银行将本金和利息自动按一年定期储蓄转存,如果存款额是100元,那么请你写出两年...
- 已知抛物线(a≠0)与x轴相交于点A,B(点A,B在原点O两侧),与y轴相交于点C,且点A,C在一次函数的图象上,线段AB长为16,线...
- 已知平面直角坐标系xOy中,点A在抛物线y=233x2+33上,过A作AB⊥x轴于点B,AD⊥y轴于点D,将矩形ABOD沿对角线BD折叠后得A的对应...
- 如图,在平行四边形ABCD中,平分,交于点,平分,交于点,与交于点,连接,.(1)求证:四边形是菱形;(2)若,,,求的值.
- 已知:如图,ABCD中,E、F分别是AD、BC的中点,求证:BE=DF。
- (本题满分10分)如图,一艘轮船由A港沿北偏东方向航行10km至B港,再沿北偏西方向航行10km到达C港. (1)求A、C两港之间的距离...