本试题 “某校高一1、2两班在一次数学考试中,成绩平均分相同,但1班的成绩比较整齐,若两班成绩的方差分别为和,则[ ]A.>B.” 主要考查您对众数、中位数、平均数
标准差、方差
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 众数、中位数、平均数
- 标准差、方差
众数:
一组数据中,出现次数最多的数据叫做这组数据的众数。
中位数:
一组数据按大小依次排列,把处在最中间位置的一个数据(或中间两个数据的平均数)叫做这组数据的中位数。
平均数:
如果有几个数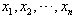 ,那么
,那么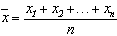 叫做这几个数的平均数。
叫做这几个数的平均数。
如果在几个数中,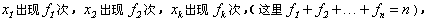 那么
那么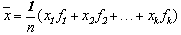 叫做这几个数的加权平均数。
叫做这几个数的加权平均数。
中位数的特点:
中位数不受少数几个极端值的影响,这在某些情况下是一个优点,但是它对极端值的不敏感有时也会成为缺点。
平均数、众数和中位数的作用:
平均数、众数和中位数都叫统计量,它们在统计中,有着广泛的应用。平均数、中位数、众数都是描述数据的集中趋势的“特征数”,平均数、中位数和众数从不同侧面给我们提供了同一组数据的面貌。
关于平均数、中位数、众数的选取:
(1)分析数据平中众,比较接近选平均,相差较大看中位,频数较大用众数;
(2)所有数据定平均,个数去除数据和,即可得到平均数;
(3)大小排列知中位;
(4)整理数据顺次排,单个数据取中问,双个数据两平均;频数最大是众数。
方差和标准差的定义:
考察样本数据的分散程度的大小,最常用的统计量是标准差。标准差是样本数据到平均数的一种平均距离,一般用s表示。
设一组数据 的平均数为
的平均数为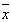 ,则
,则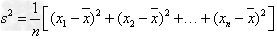 ,其中s2表示方差,s表示标准差。
,其中s2表示方差,s表示标准差。
一般地,平均数、方差、标准差具有如下性质:
若数据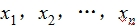 的平均数是
的平均数是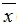 ,方差为s2,标准差为s.则新数据
,方差为s2,标准差为s.则新数据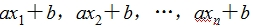 的平均数是a
的平均数是a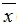 +b,方差为
+b,方差为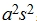 ,标准差为
,标准差为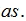
特别地,如a=1,则新数据的方差、标准差与原数据相同,分别为s2,s。因此,当一组数据均较大且接近某个常数时,可先将每个数同时减去这个常数,再计算这组新数据的方差,它与原数据的方差相等.
方差和标准差的意义:
方差和标准差都是用来描述一组数据波动情况的特征数,常数来比较两组数据的波动大小,方差较大的波动较大,方差较小的波动较小。
用样本的数字特征估计总体的数字特征分两类:
①用样本平均数估计总体平均数.
②用样本方差、标准差估计总体方差、标准差.样本容量越大,估计就越精确.
计算标准差的算法:
(1)算出样本数据的平均数;
(2)算出每个样本数据与样本平均数的差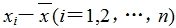 ;
;
(3)算出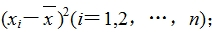
(4)算出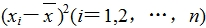 这n个数的平均数,即为样本方差s2;
这n个数的平均数,即为样本方差s2;
(5)算出方差的算术平方根,即为样本标准差s.
与“某校高一1、2两班在一次数学考试中,成绩平均分相同,但1班的成...”考查相似的试题有:
- 下列说法中,正确的是( )①数据4、6、7、7、9、4的众数是4;②一组数据的标准差是这组数据的方差的平方;③数据3,5,7,9的标...
- 为了检查一批手榴弹的杀伤半径,抽取了其中20颗做试验,得到这20颗手榴弹的杀伤半径,并列表如下: 杀伤半径(米) 7 8 9 10 ...
- 某赛季甲、乙两名运动员每场比赛得分的茎叶图(如图所示),则甲、乙两人得分的中位数之和是______.
- 一位同学种了甲、乙两种树苗各1株,分别观察了9次、10次后,得到树苗高度的数据的茎叶图如图(单位:厘米),则甲、乙两种树苗...
- 一组数据中的每一个数都乘以2,再减去3得到一组新的数据,如果求得新数据的平均数为7,方差为4,则原来数据的平均数和方差分...
- 为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6名学生进行问卷调查.6人得分情况如下:82,8...
- 下列说法错误的是( )A.在统计里,把所需考察对象的全体叫做总体B.一组数据的平均数一定大于这组数据中的每个数据C.平均...
- 某篮球队教练要从甲、乙两名运动员中挑选一名运动员,甲、乙两人进行10轮投篮比赛,每轮每人投10次,甲每轮投中的次数分别为9...
- 若数列{an}满足2an=2an-1+d(n≥2),且a1,a2,a3,a4,a5,a6,a7的方差为4,则d=______.
- 数据5,7,7,8,10,11的标准差是______.