返回

小学六年级数学

首页
首页 小学六年级数学知识 找规律 方向与位置（有序数对） 整数的四则混合运算及应用题 列方程解决问题 平行四边形的面积 试题正文
  • 解答题
    （1）用数对表示图中长方形四个顶点的位置。

    （2）实验小学举行数学竞赛，共20道题，每做对一道题得5分，做错或没做都扣2分，许明得了79分，她做对了 ____ 题。（3）按照规律填空：、、、、_________、_________。
    （4）如图，两个平行四边形的重叠部分面积相当于大平行四边形面积的，相当于小平行四边形面积的。大平行四边形与小平行四边形的面积比是_________，如果大平行四边形的面积是60平方厘米，那么，小平行四边形的面积是_______平方厘米。

    （5）小王准备去速递公司应聘，A公司每天先付20元，每投递一份邮件再付2元；B公司每投递一份邮件付3元。用m表示当天投递邮件的份数，如果到A公司应聘，每天可得工资_________；当m＞20时，去_________。
    本题信息：2011年四川省期末题数学解答题难度一般 来源:曾庆艳
  • 本题答案
    查看答案
本试题 “（1）用数对表示图中长方形四个顶点的位置。（2）实验小学举行数学竞赛，共20道题，每做对一道题得5分，做错或没做都扣2分，许明得了79分，她做对了____题。...” 主要考查您对

找规律

方向与位置（有序数对）

整数的四则混合运算及应用题

列方程解决问题

平行四边形的面积

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 找规律
  • 方向与位置（有序数对）
  • 整数的四则混合运算及应用题
  • 列方程解决问题
  • 平行四边形的面积
学习目标：
1、通过观察、实验、猜测、推理等活动发现图形的排列规律。
2、培养初步的观察、推理能力。
知识点拨：
在日常生活中，我们经常会碰到许多按一定顺序排列的数（或图形）。只要我们从不同的角度去分析研究，善于观察、分析、总结，就能发现规律，找到解决问题的方法。
找规律填数关键是根据已知的数找出数与数之间的规律。看相邻两数的倍数关系、差是常用的观察方法。
寻找数列的规律，通常从两个方面来考虑：
（1）寻找各项与项数间的关系；
（2）考虑相邻项之间的关系，然后，再总结出一般的规律。
有序数对：


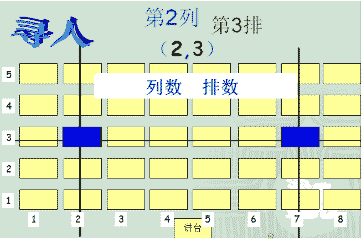
这种有顺序的两个数a和b组成的数对叫做有序数对。记作（a，b） 数对是一个表示位置的概念。前一个数字表示列，后一个数字表示行。
比如，（2，5），表示它的位置是第二列第五行。

例题解析：
下图是我校平面示意图,若科技楼所在的位置为(3，6)，则食堂所在的位置为(1，4)，宿舍楼所在的位置为(2，8)，实验楼所在的位置为(3，2)，东教学楼所在的位置为(5，2)，西教学楼所在的位置为(5，6)，办公楼所在的位置为(9，2)，大门所在的位置为(7，1)。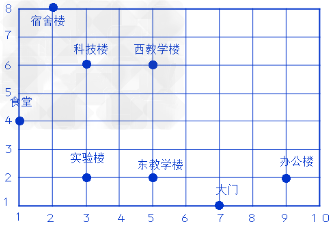


加、减、乘、除四种运算统称四则运算。
加法的意义：把两个（或几个）数合并成一个数的运算叫做加法。

减法的意义：已知两个加数的和与其中的一个加数求另一个加数的运算叫做减法。减法中，已知的两个加数的和叫做被减数，其中一个加数叫做减数，求出的另一个加数叫差。

乘法的意义：一个数乘以整数，是求几个相同加数的和的简便运算，或是求这个数的几倍是多少。

除法的意义：已知两个因数的积与其中一个因数求另一个因数的运算叫做除法。在除法中，已知的两个因数的积叫做被除数，其中一个因数叫做除数，求出的另一个因数叫商。

四则运算分为二级，加减法叫做第一级运算，乘除法叫做第二级运算。

方法点拨：
运算的顺序：在一个没有括号的算式里，如果只含有同一级运算，要从左往右依次计算；如果含有两级运算，要先算第二级运算，再算第一级运算。在有括号的算式里，要先算括号里的，再算括号外的。
列方程解决问题：
未知数用字母表示，参加列式。根据题意找出数量间的相等关系，列出含有未知数的等式，也就是方程。
它的优势体现在可以使未知数直接参加运算。
列方程解决问题一般步骤：
①审题，弄清题意：即全面分析已知数与已知数、已知数与未知数的关系。特别要把牵涉到的一些概念术语弄清，如同向，相向，增加到，增加了等。
②引进未知数：用x表示所求的数量或有关的未知量。在小学阶段所遇到的应用题并不十分复杂，一般只需要直接把要求的数量设为未知数。
③找出应用题中数量间的相等关系，列出方程。
④解方程，找出未知数的值。
⑤检验并写出答案：检验时，
一是要将所求得的未知数的值代太原方程，检验方程的解是否正确；
二是检查所求得的未知数的值是否符合题意，不符合题意的要舍去，保留符合题意的解。
平行四边形面积：
平行四边形面积=底×高，用字母表示：S=a×h。
发现相似题
与“（1）用数对表示图中长方形四个顶点的位置。（2）实验小学举...”考查相似的试题有：