本试题 “在平面上,若两个正三角形的边长的比为,则它们的面积比为1:2,类似地,在空间,若两个正四面体的棱长比为1:2,则它们的体积的比为( )” 主要考查您对柱体、椎体、台体的表面积与体积
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 柱体、椎体、台体的表面积与体积
侧面积和全面积的定义:
(1)侧面积的定义:把柱、锥、台的侧面沿着它们的一条侧棱或母线剪开,所得到的展开图的面积,就是空间几何体的侧面积.
(2)全面积的定义:空间几何体的侧面积与底面积的和叫做空间几何体的全面积,
柱体、锥体、台体的表面积公式(c为底面周长,h为高,h′为斜高,l为母线)
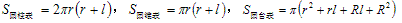
柱体、锥体、台体的体积公式:

多面体的侧面积与体积:
| 多面体 | 图像 | 侧面积 | 体积 |
| 棱柱 |
 |
直棱柱的侧面展开图是矩形 |
 |
| 棱锥 |
 |
正棱柱的侧面展开图是一些全等的等腰三角形,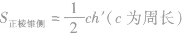 |
 |
| 棱台 |
 |
正棱台的侧面展开图是一些全等的等腰梯形,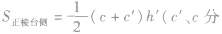  |
 |
旋转体的侧面积和体积:
| 旋转体 | 图形 | 侧面积与全面积 | 体积 |
| 圆柱 |
 |
圆柱的侧面展开图的矩形: |
 |
| 圆锥 |
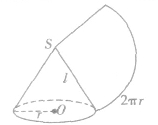 |
圆锥的侧面展开图是扇形: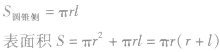 |
 |
| 圆台 |
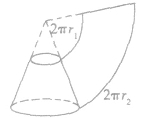 |
圆台的侧面展开图是扇环: |
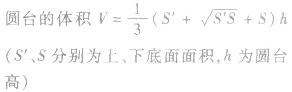 |
| 球 |
 |
 |
 |
发现相似题
与“在平面上,若两个正三角形的边长的比为,则它们的面积比为1:...”考查相似的试题有:
- 下图是某四棱锥的三视图,则该几何体的表面积等于[ ]A.34+6B.6+6+4C.6+6+4D.17+6
- 如图,一个三棱柱形容器中盛有水,且侧棱AA1=4,若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的中点,当底面AB水平...
- 如图,在长方体ABCD-A1B1C1D1中,AB=6,AD=4,AA1=3,分别过BC、A1D1的两个平行截面将长方体分成三部分,其体积分别记为若,...
- 已知三角形PAD所在平面与矩形ABCD所在平面互相垂直,PA="PD=AB=2,"若点P,A,B,C,D都在同一球面上,则此球的表面积等于( )A....
- 正四棱柱ABCD-A1B1C1D1的高为7,对角线A1C的长为5,侧面积等于______.
- 已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )cm3。
- 如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB,将剩余部分沿OC、OD折叠,使OA、OB重合,则以A、(B)、C...
- 正三棱锥的底面边长为1,侧面均为直角三角形,则此三棱锥的体积为______.
- 已知半径为的球中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是_____________
- 有一个几何体的三视图及其尺寸如下(单位cm),则该几何体的表面积和体积为[ ]A.24πcm2,12πcm3B.15πcm2,12πcm3C.24πcm2,36...