本试题 “以下3个说法中:①在同一直线上的4点A、B、C、D可以表示5条不同的线段;②大于90°的角叫做钝角;③同一个角的补角一定大于它的余角.错误说法的个数有[ ]A.0个B...” 主要考查您对直线,线段,射线
角的概念
余角,补角
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 直线,线段,射线
- 角的概念
- 余角,补角
基本概念:
直线:一根拉得很紧的线,就给我们以直线的形象,直线是直的,并且是向两方无限延伸的。一条直线可以用一个小写字母表示。
线段:直线上两个点和它们之间的部分叫做线段,这两个点叫做线段的端点。一条线段可用它的端点的两个大写字母来表示。
射线:直线上一点和它一旁的部分叫做射线。这个点叫做射线的端点。一条射线可以用端点和射线上另一点来表示。
注意:
①线和射线无长度,线段有长度。
②直线无端点,射线有一个端点,线段有两个端点。
直线、射线、线段区别:
直线没有端点,2边可无限延长;
射线有1端有端点,另一端可无限延长;
线段,有2个端点,而2个端点间的距离就是这条线段的长度。
直线除了“直”这个特点外,还有一个很重要的特点,那就是它可以向两个方向无限延伸,永远没有尽头,所以,直线是不可能度量的。因此,在画直线时,要画出没有端点的直线,表示可以无限延伸;
射线只有一个端点,可以向一个方向无限延伸,也永远没有尽头。所以,射线也是不可能度量的。直线上任意的一点可以把这条直线分成两条方向相反的射线,因此,射线是直线的一部分。虽然射线是直线的一部分,但由于它们都是不能度量的,所以,它们之间没有长短可以比较;
线段有两个端点,它有一定的长度,可以度量。线段也是直线的一部分。
各种图形表示方法:
直线:一个小写字母或两个大写字母,但前面必须加“直线”两字,如:直线l,直线m;直线AB,直线CD。
例: 直线l;直线AB。
直线l;直线AB。
射线:一个小写字母或端点的大写字母。和射线上的一个大写字母,前面必须加“射线”两字。如:射线a;射线OA。
例: 射线AB。
射线AB。
线段:用表示端点的大写字母表示,如线段AB;用一个小写字母表示,如线段a。
例: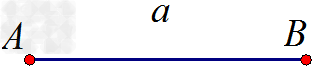 线段AB;线段a 。
线段AB;线段a 。
直线:一根拉得很紧的线,就给我们以直线的形象,直线是直的,并且是向两方无限延伸的。一条直线可以用一个小写字母表示。
线段:直线上两个点和它们之间的部分叫做线段,这两个点叫做线段的端点。一条线段可用它的端点的两个大写字母来表示。
射线:直线上一点和它一旁的部分叫做射线。这个点叫做射线的端点。一条射线可以用端点和射线上另一点来表示。
注意:
①线和射线无长度,线段有长度。
②直线无端点,射线有一个端点,线段有两个端点。
直线、射线、线段的基本性质:
| 图形 | 表示法 | 端点 | 延长线 | 能否度量 | 基本性质 | |
| 直线 | 没有端点的一条线 | 一条线, 不要端点 |
无 | 可以向两边无限延长 | 否 | 两端都没有端点,可以无限延长,不可测量的线 |
| 射线 | 只有一个端点的一条线 | 一条线, 只有一边有端点 |
一个 | 可以向一边无限延长 | 否 | 一端有端点,可以向一边无限延长,不可测量的线 |
| 线段 | 两边都有端点的一条线 | 一条线,两边都有端点 | 两个 | 不能延长 | 能 | 两端都有端点,不能延长,可测量的线 |
直线、射线、线段区别:
直线没有端点,2边可无限延长;
射线有1端有端点,另一端可无限延长;
线段,有2个端点,而2个端点间的距离就是这条线段的长度。
直线除了“直”这个特点外,还有一个很重要的特点,那就是它可以向两个方向无限延伸,永远没有尽头,所以,直线是不可能度量的。因此,在画直线时,要画出没有端点的直线,表示可以无限延伸;
射线只有一个端点,可以向一个方向无限延伸,也永远没有尽头。所以,射线也是不可能度量的。直线上任意的一点可以把这条直线分成两条方向相反的射线,因此,射线是直线的一部分。虽然射线是直线的一部分,但由于它们都是不能度量的,所以,它们之间没有长短可以比较;
线段有两个端点,它有一定的长度,可以度量。线段也是直线的一部分。
各种图形表示方法:
直线:一个小写字母或两个大写字母,但前面必须加“直线”两字,如:直线l,直线m;直线AB,直线CD。
例:
 直线l;直线AB。
直线l;直线AB。射线:一个小写字母或端点的大写字母。和射线上的一个大写字母,前面必须加“射线”两字。如:射线a;射线OA。
例:
 射线AB。
射线AB。线段:用表示端点的大写字母表示,如线段AB;用一个小写字母表示,如线段a。
例:
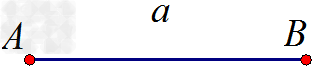 线段AB;线段a 。
线段AB;线段a 。角的基本概念:
从静态角度认识角:由一个点出发的两条射线组成的图形叫角;
从动态角度认识角:一条射线绕着它的顶点旋转到另一个位置,则这两条射线组成的图像叫角。有公共端点的两条射线组成的图形叫做角,这个公共端点叫做角的顶点,这两条射线叫做角的边。
①因为射线是向一方无限延伸的,所以角的两边无所谓长短,即角的大小与它的边长无关。
②角的大小可以度量,可以比较。
③根据角的度数,角可以分为锐角、直角、钝角、平角、周角。
角的表示:角可以用大写英文字母、阿拉伯数字或小写的希腊字母表示,如∠1,∠α,∠BAD等。
角的分类:
根据角的度数,角可以分为锐角、直角、钝角、平角、周角。
平角:180。的角,当角的两边在一条直线上时,组成的角叫做平角。即射线OA绕点O旋转,当终边在始边OA的反向延长线上时所成的角;
直角:90。的角,即线OA绕点O旋转,当终边与始边垂直时所成的角,平角的一半叫做直角;
锐角:大于0。小于90。的角,小于直角的角叫做锐角;
钝角:大于90。小于180。的角,大于直角且小于平角的角叫做钝角。
周角:360。的角,即射线OA绕点O旋转,当终边与始边重合时所成的角。
角的性质:
①角的大小与边的长短无关,只与构成角的两条射线的幅度大小有关;
②角的大小可以度量,可以比较;
③角可以参与运算。
角的度量:
角的度量有如下规定:把一个平角180等分,每一份就是1度的角,单位是度,用“。”,1度记作“1°”,n度记作“n°”。把1°的角60等分,每一份叫做1分的角,1分记作“1′”。把1′的角60等分,每一份叫做1秒的角,1秒记作“1″”。1°=60′=3600″。
余角:
如果两个角的和是一个直角,那么称这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角。
∠A +∠C=90°,∠A= 90°-∠C ,∠C的余角=90°-∠C 即:∠A的余角=90°-∠A
补角:
如果两个角的和是一个平角,那么这两个角叫互为补角.其中一个角叫做另一个角的补角
∠A +∠C=180°,∠A= 180°-∠C ,∠C的补角=180°-∠C 即:∠A的补角=180°-∠A
补角的性质:
同角的补角相等。比如:∠A+∠B=180°,∠A+∠C=180°,则:∠C=∠B。
等角的补角相等。比如:∠A+∠B=180°,∠D+∠C=180°,∠A=∠D则:∠C=∠B。
余角的性质:
同角的余角相等。比如:∠A+∠B=90°,∠A+∠C=90°,则:∠C=∠B。
等角的余角相等。比如:∠A+∠B=90°,∠D+∠C=90°,∠A=∠D则:∠C=∠B。
注意:
①钝角没有余角;
②互为余角、补角是两个角之间的关系。如∠A+∠B+∠C=90°,不能说∠A、∠B、∠C互余;同样:如∠A+∠B+∠C=180°,不能说∠A、∠B、∠C互为补角;
③互为余角、补角只与角的度数相关,与角的位置无关。只要它们的度数之和等于90°或180°,就一定互为余角或补角。
余角与补角概念认识提示:
(1)定义中的“互为”一词如何理解?
如果∠1与∠2互余,那么∠1的余角是∠2 ,同样∠2的余角是∠1 ;如果∠1与∠2互补,那么∠1的补角是∠2 , 同样∠2的补角是∠1。
(2)互余、互补的两角是否一定有公共顶点或公共边?
两角互余或互补,只与角的度数有关,与位置无关。
(3)∠1 + ∠2 + ∠3 = 90°(180°),能说∠1 、∠2、 ∠3 互余(互补)吗?
不能,互余或互补是两个角之间的数量关系。
发现相似题
与“以下3个说法中:①在同一直线上的4点A、B、C、D可以表示5条不...”考查相似的试题有:
- 已知线段AB,在AB的延长线上取一点C,使AC=2BC,在AB的反向延长线上取一点D,使DA=2AB,那么线段AC是线段DB的( )倍.A.23B...
- 已知A、O、B三点在同一直线上。OA=2,OB=3,则AB两点之间的距离是( )。
- 点P为直线l外一点,点A、B、C为直线l上三点,PA=4cm,PB=5cm,PC=2cm,则点到直线l的距离是( )A.2cmB.小于2cmC.不大于2cmD.4cm
- 如图,线段AB上有两点C、D,则图中有( )条线段.A.3B.4C.5D.6
- 下列说法错误的是( )A.过一点有且只有一条直线与已知直线平行B.两点之间的所有连线中,线段最短C.经过两点有且只有一条直线...
- 从3时到6时,钟表的时针旋转角的度数是( )A.30B.60°C.90°D.120°
- 若∠1:∠2:∠3=1:2:3,且∠1+∠2+∠3=180°,则∠2=( ).
- 如果小樱家在小欢家的北偏东60°的方向上,那么小欢家在小樱家的______.
- 已知∠=35°45′,则∠的补角=( )。
- 76°角的补角是( )