本试题 “已知函数f(x)=tan(2x-bπ)的图象的一个对称中心为(,0),若|b|<,则f(x)的解析式为( ) A.tan(2x+) B.tan(2x-) C.tan(2x+)或tan(2x-) D...” 主要考查您对正切、余切函数的图象与性质(定义域、值域、单调性、奇偶性等)
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 正切、余切函数的图象与性质(定义域、值域、单调性、奇偶性等)
正切函数的图像:
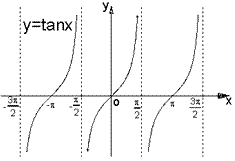
余切函数的图像:
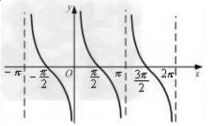
正切函数的性质:
(1)定义域: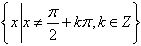 ;
;
(2)值域是R,在上面定义域上无最大值也无最小值;
(3)周期性:是周期函数且周期是π,它与直线y=a的两个相邻交点之间的距离是一个周期π;
(4)奇偶性:是奇函数,对称中心是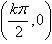 (k∈Z),无对称轴;
(k∈Z),无对称轴;
(5)单调性:正切函数在开区间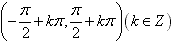 内都是增函数。但要注意在整个定义域上不具有单调性。
内都是增函数。但要注意在整个定义域上不具有单调性。
余切函数的性质:
(1)定义域:{x|x≠kπ,k∈Z}
(2)值域:实数集R;
(3)周期性:是周期函数,周期为kπ(k∈Z且k≠0),最小正周期T=π
(4)奇偶性:奇函数,图像关于( ,0)(k∈z)对称,实际上所有的零点都是它的对称中心
,0)(k∈z)对称,实际上所有的零点都是它的对称中心
(5)单调性:在每一个开区间(kπ,(k+1)π),(k∈Z)上都是减函数,在整个定义域上不具有单调性
发现相似题
与“已知函数f(x)=tan(2x-bπ)的图象的一个对称中心为(,0)...”考查相似的试题有:
- 函数的值域是 ▲
- 画在同一坐标系内的曲线的交点坐标是( )A.B.C.D.
- 已知函数,()的最大值为,求的表达式
- 已知函数,.求:(1)函数的最小值及取得最小值的自变量的集合;(2)函数的单调增区间.
- 函数的值域是( )A {-1,0,1,3} B {-1,0,3} C {-1,3} D {-1,1}
- 函数,为增函数的区间是( )A.B.C.D.
- 已知函数在一个周期内的图象如图所示.则的图象可由函数y=cosx的图象(纵坐标不变) ( )A.先把各点的横坐标缩短到原来的倍,...
- 函数的最大值是( )A.3B.C.2D.
- 已知函数,在下列四个命题中:①函数的最小正周期是;②函数的表达式可以改写为;③若,且,则;④对任意的实数,都有成立;其中...
- 已知直线y=b(b