本试题 “若f(x)=tan(x+),则( ) A.f(-1)>f(0)>f(1) B.f(0)>f(1)>f(-1) C.f(1)>f(0)>f(-1) D.f(0)>f(-1)>f(1)” 主要考查您对正切、余切函数的图象与性质(定义域、值域、单调性、奇偶性等)
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 正切、余切函数的图象与性质(定义域、值域、单调性、奇偶性等)
正切函数的图像:
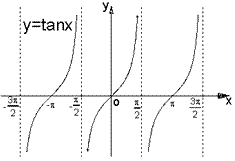
余切函数的图像:
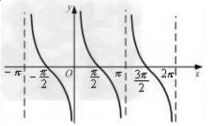
正切函数的性质:
(1)定义域: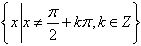 ;
;
(2)值域是R,在上面定义域上无最大值也无最小值;
(3)周期性:是周期函数且周期是π,它与直线y=a的两个相邻交点之间的距离是一个周期π;
(4)奇偶性:是奇函数,对称中心是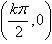 (k∈Z),无对称轴;
(k∈Z),无对称轴;
(5)单调性:正切函数在开区间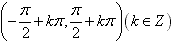 内都是增函数。但要注意在整个定义域上不具有单调性。
内都是增函数。但要注意在整个定义域上不具有单调性。
余切函数的性质:
(1)定义域:{x|x≠kπ,k∈Z}
(2)值域:实数集R;
(3)周期性:是周期函数,周期为kπ(k∈Z且k≠0),最小正周期T=π
(4)奇偶性:奇函数,图像关于( ,0)(k∈z)对称,实际上所有的零点都是它的对称中心
,0)(k∈z)对称,实际上所有的零点都是它的对称中心
(5)单调性:在每一个开区间(kπ,(k+1)π),(k∈Z)上都是减函数,在整个定义域上不具有单调性
发现相似题
与“若f(x)=tan(x+),则( ) A.f(-1)>f(0)>f(1) B.f...”考查相似的试题有:
- 已知函数,(Ⅰ)求函数的最大值和最小正周期;(Ⅱ)设的内角的对边分别且,,若求的值.
- 已知, 则= 。
- 已知向量,,且的最小正周期为(Ⅰ)求的值;(Ⅱ)若,解方程;(Ⅲ)在中,,,且为锐角,求实数的取值范围.
- 已知角φ的终边经过点P(1,-1),点A(x1,y1)、B(x2,y2)是函数f(x)=sin(ωx+φ)(ω>0)图象上的任意两点.若|f(x1)-f(x2)|=2...
- 函数的图象大致是( )
- 下列四个函数中,以π为最小正周期,且在区间(,π)上为减函数的是[ ]A.B.y=2|sinx|C.D.y=-ctgx
- 设函数f(x)=a·b,其中向量a=(cos,sin),(x∈R),向量b=(cosj,sinj)(Ⅰ)求j的值;(Ⅱ)若函数y=1+sin的图象按向...
- 关于函数f(x)=sin2x-()|x|+,有下面四个结论,其中正确结论的个数为( )①f(x)是奇函数; ②当x>2009时,f(x)>恒成...
- 平面上有两个定点A,B,另有4个与A,B不重合的动点C1,C2,C3,C4。若使,则称()为一个好点对.那么这样的好点对( )A.不存...
- 已知,则式子的值为( )A.B.C.D.