本试题 “下列说法正确的个数:①;②的倒数是﹣3;③;④的平方根是4[ ]A.0个B.1个C.2个D.3个” 主要考查您对倒数
二次根式的加减
平方根
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 倒数
- 二次根式的加减
- 平方根
倒数的定义:
如果两个数的乘积等于1,那么这两个数就叫做互为倒数。
倒数性质:
(1)若a、b互为倒数,则ab=1,或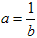 ,反之也成立;
,反之也成立;
(2)0没有倒数;
(3)乘积为-1的两个数互为负倒数,即ab=-1,则ab互为负倒数,反之也成立。
倒数的特点:
一个正实数(1除外)加上它的倒数 一定大于2。
理由:a/b,b/a为倒数当a>b时a/b一定大于1,可写为1+(a-b)/b。因为:
b/a+(a-b)/a
=b×b/a×b+(a÷b-b×b)/ab
=(a×a-b×b+b×b)/ab
=a×a/a×b,
又因为a>b,
所以a·a>a·b,
所以a·a/a·b>1,
所以1+(a-b)/b+a·a/a·b>2,
所以一个正实数加上它的倒数一定大于2。
当b>a时也一样。
同理可证,一个负实数(-1除外)加上它的倒数一定小于-2。
倒数的求法:
1.求一个分数的倒数,例如3/4,我们只须把3/4这个分数的分子和分母交换位置,即得3/4的倒数为4/3。
2.求一个整数的倒数,只须把这个整数看成是分母为1的分数,然后再按求分数倒数的方法即可得到。
如12,即12/1,再把12/1这个分数的分子和分母交换位置,把分子做分母,分母做分子,则有1/12。 即12倒数是1/12。
说明:倒数是本身的数是1和-1。(0没有倒数)
把0.25化成分数,即1/4
再把1/4这个分数的分子和分母交换位置,把原来的分子做分母,原来的分母做分子.则是4/1
再把4/1化成整数,即4
所以0.25是4的倒数。也可以说4是0.25的倒数
也可以用1去除以这个数,例如0.25
1/0.25等于4
所以0.25的倒数4.
因为乘积是1的两个数互为倒数。
分数、整数也都使不完整用这种规律。
如果两个数的乘积等于1,那么这两个数就叫做互为倒数。
倒数性质:
(1)若a、b互为倒数,则ab=1,或
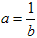 ,反之也成立;
,反之也成立;(2)0没有倒数;
(3)乘积为-1的两个数互为负倒数,即ab=-1,则ab互为负倒数,反之也成立。
倒数的特点:
一个正实数(1除外)加上它的倒数 一定大于2。
理由:a/b,b/a为倒数当a>b时a/b一定大于1,可写为1+(a-b)/b。因为:
b/a+(a-b)/a
=b×b/a×b+(a÷b-b×b)/ab
=(a×a-b×b+b×b)/ab
=a×a/a×b,
又因为a>b,
所以a·a>a·b,
所以a·a/a·b>1,
所以1+(a-b)/b+a·a/a·b>2,
所以一个正实数加上它的倒数一定大于2。
当b>a时也一样。
同理可证,一个负实数(-1除外)加上它的倒数一定小于-2。
倒数的求法:
1.求一个分数的倒数,例如3/4,我们只须把3/4这个分数的分子和分母交换位置,即得3/4的倒数为4/3。
2.求一个整数的倒数,只须把这个整数看成是分母为1的分数,然后再按求分数倒数的方法即可得到。
如12,即12/1,再把12/1这个分数的分子和分母交换位置,把分子做分母,分母做分子,则有1/12。 即12倒数是1/12。
说明:倒数是本身的数是1和-1。(0没有倒数)
把0.25化成分数,即1/4
再把1/4这个分数的分子和分母交换位置,把原来的分子做分母,原来的分母做分子.则是4/1
再把4/1化成整数,即4
所以0.25是4的倒数。也可以说4是0.25的倒数
也可以用1去除以这个数,例如0.25
1/0.25等于4
所以0.25的倒数4.
因为乘积是1的两个数互为倒数。
分数、整数也都使不完整用这种规律。
二次根式加减法法则:
先把式子中各项二次根式化成最简二次根式,然后再合并同类二次根式。
1、同类二次根式
一般地,把几个二次根式化为最简二次根式后,如果它们的被开方数相同,就把这几个二次根式叫做同类二次根式。
2、合并同类二次根式
把几个同类二次根式合并为一个二次根式就叫做合并同类二次根式。
3、二次根式加减时,可以先将二次根式化为最简二次根式,再将被开方数相同的进行合并。
例如:(1);2 +3
+3 =5
=5 (2)
(2)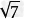 +2
+2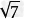 =3
=3
4、注意:有括号时,要先去括号。
二次根式的加减注意:
①二次根式合并同类项与合并同类项类似,因此二次根式的加减可以对比整式的加减进行;
②二次根式加减混合运算的是指就是合并同类项二次根式,不是同类二次根式不能合并。如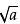 +
+ 是最简结果,不能再合并;
是最简结果,不能再合并;
③二次根式进行加减运算时,根号外的系数因式须保留假分数形式,如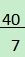
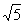 ,不能写成5
,不能写成5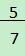
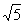
④合并同类二次根式后若系数为多项式,须添加括号。
先把式子中各项二次根式化成最简二次根式,然后再合并同类二次根式。
1、同类二次根式
一般地,把几个二次根式化为最简二次根式后,如果它们的被开方数相同,就把这几个二次根式叫做同类二次根式。
2、合并同类二次根式
把几个同类二次根式合并为一个二次根式就叫做合并同类二次根式。
3、二次根式加减时,可以先将二次根式化为最简二次根式,再将被开方数相同的进行合并。
例如:(1);2
 +3
+3 =5
=5 (2)
(2)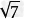 +2
+2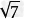 =3
=3
4、注意:有括号时,要先去括号。
二次根式的加减注意:
①二次根式合并同类项与合并同类项类似,因此二次根式的加减可以对比整式的加减进行;
②二次根式加减混合运算的是指就是合并同类项二次根式,不是同类二次根式不能合并。如
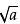 +
+ 是最简结果,不能再合并;
是最简结果,不能再合并;③二次根式进行加减运算时,根号外的系数因式须保留假分数形式,如
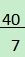
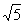 ,不能写成5
,不能写成5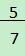
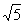
④合并同类二次根式后若系数为多项式,须添加括号。
平方根定义:
如果一个数的平方等于a,则这个数叫做a的平方根,如果x2=a,那么x叫做a的平方根,这里a是x的平方,它是一个非负数,即a≥0。
表示:一个正数有两个平方根,用 表示平方根中正的那个,用-
表示平方根中正的那个,用-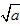 表示负的平方根。
表示负的平方根。
1 至 20 的平方根:
利用长式除法可以求平方根。长式除法需要进行加法,减法,乘法,除法等四则运算。一般计算机软件的运算精度小于20位数字,如要计算平方根到100位,四则运算的精度需100位以上。 利用高精度长式除法可以计算出 1 至 20 的 平方根如下:
其中,有两数的根号可借由“口诀”记忆: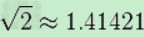 (意思意思而已),
(意思意思而已), (一妻三儿、一起散热)。
(一妻三儿、一起散热)。
如果一个数的平方等于a,则这个数叫做a的平方根,如果x2=a,那么x叫做a的平方根,这里a是x的平方,它是一个非负数,即a≥0。
表示:一个正数有两个平方根,用
 表示平方根中正的那个,用-
表示平方根中正的那个,用-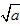 表示负的平方根。
表示负的平方根。性质:
①一个正数如果有平方根,那么必定有两个,它们互为相反数。
显然,如果我们知道了这两个平方根的一个,那么就可以及时的根据相反数的概念得到它的另一个平方根。
②如果一个正数x的平方等于a,即x的平方等于a,那么这个正数x叫做a的算术平方根。a
的算术平方根记为,读作“根号a”,a叫做被开方数。
③规定:0的平方根是0。
④负数在实数范围内不能开平方,只有在复数范围内,才可以开平方根。
例如:-1的平方根为±1,-9的平方根为±3。
⑤平方根包含了算术平方根,算术平方根是平方根中的一种。
平方根和算术平方根都只有非负数才有。
被开方数是乘方运算里的幂。
求平方根可通过逆运算平方来求。
开平方:求一个非负数a的平方根的运算叫做开平方,其中a叫做被开方数。
若x的平方等于a,那么x就叫做a的平方根,即正负根号a=正负x
1 至 20 的平方根:
利用长式除法可以求平方根。长式除法需要进行加法,减法,乘法,除法等四则运算。一般计算机软件的运算精度小于20位数字,如要计算平方根到100位,四则运算的精度需100位以上。 利用高精度长式除法可以计算出 1 至 20 的 平方根如下:
 |
=1 |
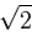 |
≈1.414213562373095048801688724209698078569671875376948073176679737990732478462 |
 |
≈1.732050807568877293527446341505872366942805253810380628055806979451933016909 |
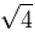 |
=2 |
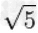 |
≈2.236067977499789696409173668731276235440618359611525724270897245410520925638 |
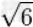 |
≈2.449489742783178098197284074705891391965947480656670128432692567250960377457 |
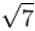 |
≈2.645751311064590590501615753639260425710259183082450180368334459201068823230 |
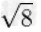 |
≈2.828427124746190097603377448419396157139343750753896146353359475981464956924 |
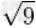 |
=3 |
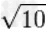 |
≈3.162277660168379331998893544432718533719555139325216826857504852792594438639 |
 |
≈3.316624790355399849114932736670686683927088545589353597058682146116484642609 |
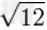 |
≈3.464101615137754587054892683011744733885610507620761256111613958903866033818 |
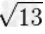 |
≈3.605551275463989293119221267470495946251296573845246212710453056227166948293 |
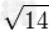 |
≈3.741657386773941385583748732316549301756019807778726946303745467320035156307 |
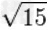 |
≈3.872983346207416885179265399782399610832921705291590826587573766113483091937 |
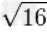 |
≈4 |
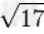 |
≈4.123105625617660549821409855974077025147199225373620434398633573094954346338 |
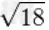 |
≈4.242640687119285146405066172629094235709015626130844219530039213972197435386 |
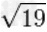 |
≈4.358898943540673552236981983859615659137003925232444936890344138159557328203 |
 |
≈4.472135954999579392818347337462552470881236719223051448541794490821041851276 |
其中,有两数的根号可借由“口诀”记忆:
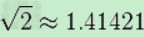 (意思意思而已),
(意思意思而已), (一妻三儿、一起散热)。
(一妻三儿、一起散热)。 发现相似题
与“下列说法正确的个数:①;②的倒数是﹣3;③;④的平方根是4[ ]A...”考查相似的试题有: