返回

高中数学

首页
首页 高中数学知识 函数的奇偶性、周期性 空间中直线与平面的位置关系 相等向量与共线向量的定义 试题正文
  • 填空题
    下列命题中，错误命题的序号有______．
    （1）“a=-1”是“函数f（x）=x2+|x+a+1|（ x∈R） 为偶函数”的必要条件；
    （2）“直线l垂直平面α内无数条直线”是“直线l垂直平面α”的充分条件；
    （3）已知a，b，c为非零向量，则“a•b=a•c”是“b=c”的充要条件；
    （4）若p：∃x∈R，x2+2x+2≤0，则￢p：∀x∈R，x2+2x+2＞0．
    本题信息：数学填空题难度一般 来源:未知
  • 本题答案
    查看答案
本试题 “下列命题中，错误命题的序号有______．（1）“a=-1”是“函数f（x）=x2+|x+a+1|（ x∈R） 为偶函数”的必要条件；（2）“直线l垂直平面α内无数条直线”是“直线l垂直...” 主要考查您对

函数的奇偶性、周期性

空间中直线与平面的位置关系

相等向量与共线向量的定义

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 函数的奇偶性、周期性
  • 空间中直线与平面的位置关系
  • 相等向量与共线向量的定义

函数的奇偶性定义：

偶函数：一般地，如果对于函数f（x）的定义域内任意一个x，都有f（-x）=f（x），则称函数f（x）为偶函数。
奇函数：一般地，如果对于函数f（x）的定义域内任意一个x，都有f（-x）＝-f（x），那么函数f（x）是奇函数。 
 
函数的周期性：

（1）定义：若T为非零常数，对于定义域内的任一x，使f（x+T）=f（x）恒成立，则f（x）叫做周期函数，T叫做这个函数的一个周期。
周期函数定义域必是无界的。
（2）若T是周期，则k·T（k≠0，k∈Z）也是周期，所有周期中最小的正数叫最小正周期。一般所说的周期是指函数的最小正周期。
周期函数并非都有最小正周期，如常函数f（x）=C。


奇函数与偶函数性质：

（1）奇函数与偶函数的图像的对称性：奇函数的图像关于原点对称，偶函数的图像关于y轴对称。
（3）在公共定义域内，①两个奇函数的和是奇函数，两个奇函数的积是偶函数； ②两个偶函数的和、积是偶函数； ③一个奇函数，一个偶函数的积是奇函数。

注：定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件．


1、函数是奇函数或偶函数的前提定义域必须关于原点对称；定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件．

2、函数的周期性    令a , b 均不为零，若： 
（1）函数y = f(x) 存在 f(x)=f(x + a) ==> 函数最小正周期 T=|a| 
（2）函数y = f(x) 存在f(a + x) = f(b + x) ==> 函数最小正周期 T=|b-a| 
（3）函数y = f(x) 存在 f(x) = -f(x + a) ==> 函数最小正周期 T=|2a| 
（4）函数y = f(x) 存在 f(x + a) =  ==> 函数最小正周期 T=|2a| 
（5）函数y = f(x) 存在 f(x + a) = 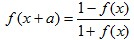  ==> 函数最小正周期 T=|4a|


空间中直线与平面的位置关系有且只有三种：

1、直线在平面内——有无数个公共点；
2、直线与平面相交——有且只有一个公共点；
3、直线与平面平行——没有公共点。
直线与平面相交和平行统称为直线在平面外。
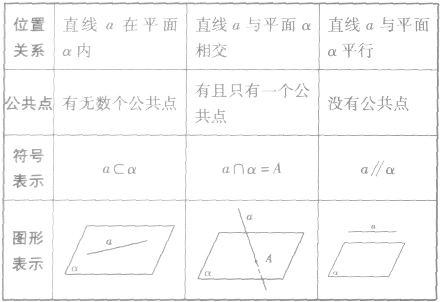
直线和平面的位置关系符号表示及相应的图形见下表：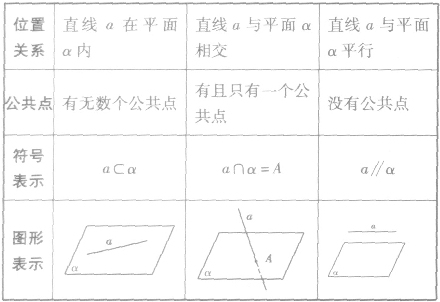


直线和平面的位置关系符号表示及相应的图形见下表：


相等向量的定义：

长度相等且方向相同的两个向量叫相等向量。

共线向量的定义：

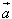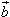方向相同或相反的非零向量，平行于，记作：。
规定零向量和任何向量平行。
注意：相等向量一定是共线向量，但共线向量不一定相等。表示共线向量的有向线段不一定在同一直线上，向量可以平移。


平行向量与相等向量的关系：

(l)平行向量只要求方向相同或相反即可，用有向线段表示平行向量时，向量所在的直线重合或平行．
(2)平行向量要求两个向量均为非零向量，规定：零向量与任一向量平行，记作；相等向量则没有这个限制，零向量与零向量相等．
(3)借助相等向量，可以把一组平行向量移动到同一直线上，因此，平行向量也叫做共线向量．(4)平行向量不一定是相等向量，但相等向量一定是平行向量．


向量共线的理解：

(1)两个非零向量平行的充要条件是这两个向量所在直线平行或重合．
(2)两个平行的非零向量在其方向与模两个要素上可能出现以下四种情况：
①方向相同，长度相同；
②方向相同，长度不同；
③方向相反，长度相同；
④方向相反，长度不同，

两个向量相等的理解：

(1)两个向量的长度相等，这两个向量不一定相等．
(2)两个向量相等，它们的起点和终点不一定相同．
(3)若a=b，b=c，则必有a=c．


发现相似题
与“下列命题中，错误命题的序号有______．（1）“a=-1”是“函数f（...”考查相似的试题有：