本试题 “已知a、b为一等腰三角形的两边长,且满足等式23a-6+32-a=b-4,则此等腰三角形的周长是______.” 主要考查您对二次根式的定义
等腰三角形的性质,等腰三角形的判定
三角形的三边关系
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 二次根式的定义
- 等腰三角形的性质,等腰三角形的判定
- 三角形的三边关系
我们把形如
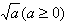 叫做二次根式。
叫做二次根式。二次根式必须满足:
含有二次根号“
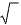 ”;
”;被开方数a必须是非负数。
确定二次根式中被开方数的取值范围:
要是二次根式
 有意义,被开方数a必须是非负数,即a≥0,由此可确定被开方数中字母的取值范围。
有意义,被开方数a必须是非负数,即a≥0,由此可确定被开方数中字母的取值范围。 二次根式性质:
(1)a≥0 ;
 ≥0 (双重非负性 );
≥0 (双重非负性 );(2)
 ;
;(3)
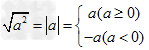
0(a=0);
(4)
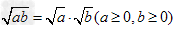 ;
;(5)
 。
。二次根式判定:
①二次根式必须有二次根号,如 ,
,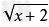 等;
等;
②二次根式 中,被开方数a可以是具体的一个数,也可以是代数式;
中,被开方数a可以是具体的一个数,也可以是代数式;
③二次根式定义中a≥0 是定义组成的一部分,不能省略;
④二次根式 是一个非负数;
是一个非负数;
⑤二次根式与算术平方根有着内在的联系, (a≥0 )就表示a的算术平方根。
(a≥0 )就表示a的算术平方根。
二次根式的应用:
主要体现在两个方面:
(1)利用从特殊到一般,在由一般到特殊的重要思想方法,解决一些规律探索性问题;
(2)利用二次根式解决长度、高度计算问题,根据已知量,求出一些长度或高度,或设计省料的方案,以及图形的拼接、分割问题。这个过程需要用到二次根式的计算,其实就是化简求值。
有两条边相等的三角形,是等腰三角形,相等的两条边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
等腰三角形的性质:
1.等腰三角形的两个底角度数相等(简写成“等边对等角”)。
2.等腰三角形的顶角的平分线,底边上的中线,底边上的高重合(简写成“等腰三角形的三线合一”)。
3.等腰三角形的两底角的平分线相等(两条腰上的中线相等,两条腰上的高相等)。
4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高(需用等面积法证明)。
7.等腰三角形是轴对称图形,只有一条对称轴,顶角平分线所在的直线是它的对称轴,等边三角形有三条对称轴。
8.等腰三角形中腰的平方等于高的平方加底的一半的平方
9.等腰三角形中腰大于高
10.等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高(需用等面积法证明)
等腰三角形的判定:
1.定义法:在同一三角形中,有两条边相等的三角形是等腰三角形。
2.判定定理:在同一三角形中,有两个角相等的三角形是等腰三角形(简称:等角对等边)。
3.顶角的平分线,底边上的中分线,底边上的高的重合的三角形是等腰三角形。
三角形的三边关系:
在三角形中,任意两边和大于第三边,任意两边差小于第三边。
设三角形三边为a,b,c
则
a+b>c
a+c>b
b+c>a
a-b<c
a-c<b
b-c<a
在直角三角形中,设a、b为直角边,c为斜边。
则两直角边的平方和等于斜边平方。
在等边三角形中,a=b=c
在等腰三角形中, a,b为两腰,则a=b
在三角形ABC的内角A、B、C所对边分别为a、b、c的情况下,c2=a2+b2-2abcosc
三角形的三边关系定理及推论:
(1)三角形三边关系定理:三角形的两边之和大于第三边。
推论:三角形的两边之差小于第三边。
(2)三角形三边关系定理及推论的作用:
①判断三条已知线段能否组成三角形;
②当已知两边时,可确定第三边的范围;
③证明线段不等关系。
与“已知a、b为一等腰三角形的两边长,且满足等式23a-6+32-a=b-4...”考查相似的试题有:
- 计算: .
- 的值是( )A.2B.±2C.-2D.0
- 若a2+a=0,则a的取值范围为______.
- 若式子在实数范围内有意义,则x的取值范围是A.x>1B.x
- 等腰三角形的两边长为4和7,则这个三角形的周长是( )A.15B.18C.15或18D.无法计算
- 下列命题中,其逆否命题是真命题的命题个数有( )(1)线段垂直平分线上的任意一点到这条线段两个端点的距离相等;(2)对顶...
- 等腰三角形的周长为19cm,其中一边长为5cm,则该等腰三角形的底边边长为( )A.9cmB.5cmC.9cm或5cmD.10cm
- 已知△ABC中,AB=3,BC=4,则第三边AC的取值范围是( )A.3<AC<4B.1≤AC≤7C.1<AC<7D.0<AC<12
- 如果三角形的两边分别为7和2,且它的周长为偶数,那么第三边的长为[ ]A.5B.6C.7D.8
- 下列每组数字分别是三根小木棒的长度,则能摆成三角形的是( )A.3、4、8B.8、7、15C.13、12、20D.5、5、11