本试题 “在△ABC中,a=2,b=3,C=135°,则△ABC的面积等于 ( )A.B.3C.D.3” 主要考查您对解三角形
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 解三角形
解三角形定义:
一般地,把三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素。已知三角形的几个元素求其他元素的过程叫做解三角形。
主要方法:
正弦定理、余弦定理。
解三角形常用方法:
1.已知一边和两角解三角形:已知一边和两角(设为b、A、B),解三角形的步骤:
2.已知两边及其中一边的对角解三角形:已知三角形两边及其中一边的对角,求该三角形的其他边角时,首先必须判断是否有解,例如在 中,已知
中,已知![]()
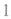 ,问题就无解。如果有解,是一解,还是两解。解得个数讨论见下表:
,问题就无解。如果有解,是一解,还是两解。解得个数讨论见下表:
3.已知两边及其夹角解三角形:已知两边及其夹角(设为a,b,C),解三角形的步骤: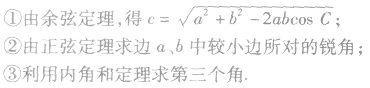
4.已知三边解三角形:已知三边a,b,c,解三角形的步骤:
①利用余弦定理求出一个角;
②由正弦定理及A +B+C=π,求其他两角.
5.三角形形状的判定:
判断三角形的形状,应围绕三角形的边角关系进行思考,主要看其是否是正三角形、等腰三角形、直角三角形、钝角三角形、锐角三角形,要特别注意“等腰直角三角形”与“等腰三角形或直角三角形”的区别,依据已知条件中的边角关系判断时,主要有如下两条途径:
①利用正、余弦定理把已知条件转化为边边关系,通过因式分解、配方等得出边的相应关系,从而判断三角形的形状;
②利用正、余弦定理把已知条件转化为内角的三角函数间的关系,通过三角函数的恒等变形,得出内角的关系,从而判断出三角形的形状,此时要注意应用A+B +C=π这个结论,在以上两种解法的等式变形中,一般两边不要约去公因式,应移项提取公因式,以免漏解.
6.解斜三角形应用题的一般思路:
(1)准确理解题意,分清已知与所求,准确理解应用题中的有关名称、术语,如坡度、仰角、俯角、视角、象限角、方位角、方向角等;
(2)根据题意画出图形;
(3)将要求解的问题归结到一个或几个三角形中,通过合理运用正弦定理、余弦定理等有关知识建立数学模型,然后正确求解,演算过程要算法简练,计算准确,最后作答,
用流程图可表示为: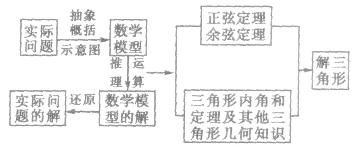
利用正弦定理、余弦定理在解决三角形的综合问题时,要注意三角形三内角的一些三角函数关系:
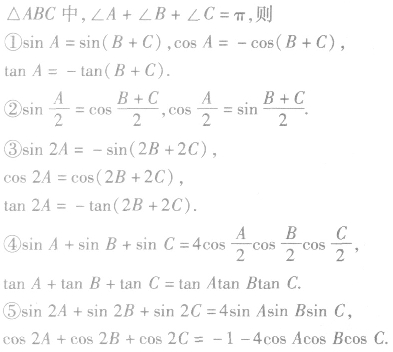
与“在△ABC中,a=2,b=3,C=135°,则△ABC的面积等于 ( )A.B.3C...”考查相似的试题有:
- △ABC中,如果,,S△ABC=4,那么=( )A.B.C.D.
- (12分)在锐角三角形ABC中,∠A,∠B,∠C的对边分别为a,b,c,且b2+c2=bc+a2(1)求∠A;(2)若a=,求b2+c2的取值范围。
- (本题满分12分)已知、、为的三个内角,且其对边分别为、、,若 (1)求角的值;20090520 (2)若的面积.
- 在△ABC中,角A,B,C所对的边分别为a,b,c,且B=π3,cosC=13,b=36.( I)求c的值;( II)求△ABC的面积.
- △ABC的内角A,B,C对边分别是a,b,c,且,.(1)求角A与角B的大小;(2)若BC边上的中线AM的长为,求△ABC的面积.
- (本小题12分)已知满足.(1)将表示为的函数,并求的单调递增区间;(2)已知三个内角、、的对边分别为、、,若,且,求面积...
- 已知的面积是,内角所对边分别为,.若,则的值是 ★ .
- 在中分别为的对边,若,则为 三角形.
- 将函数y=的图像向左平移个单位,再向上平移1个单位,得到的图像,则的值是( )A.B.C.D.
- 在△ABC中若则△ABC是( )A.等边三角形B.直角三角形C.钝角三角形D.等腰直角三角形