本试题 “一个等腰三角形的一边长为1,另一边长为,则等腰三角形的周长是( ) A.2+ B.1+2 C.2 D.2或3” 主要考查您对估算无理数的大小
等腰三角形的性质,等腰三角形的判定
三角形的三边关系
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 估算无理数的大小
- 等腰三角形的性质,等腰三角形的判定
- 三角形的三边关系
在一些题目中我们常常需要估算无理数的取值范围,要想准确地估算出无理数的取值范围需要记住一些常用数的平方。一般情况下从1到达20整数的平方都应牢记。
例:估算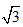 的取值范围。
的取值范围。
解:因为1<3<4,所以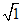 <
< <
< ,
,
即:1<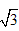 <2如果想估算的更精确一些,
<2如果想估算的更精确一些,
比如说想精确到0.1.可以这样考虑:因为17的平方是289,18的平方是324,所以1.7的平方是2.89,1.8的平方是3.24.
因为2.89<3<3.24,
所以 <
<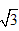 <
<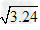 ,
,
所以1.7<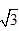 <1.8。
<1.8。
如果需要估算的数比较大,可以找几个比较接近的数值验证一下。
比较无理数大小的几种方法:
比较无理数大小的方法很多,在解题时,要根据所给无理数的特点,选择合适的比较方法。
一、直接法
直接利用数的大小来进行比较。
①、同是正数:
例: 与3的比较
与3的比较
根据无理数和有理数的联系,被开数大的那个就大。
因为3=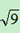 >
> ,所以3>
,所以3>
②、 同是负数:
根据无理数和有理数的联系,及同是负数绝对值大的反而小。
③、 一正一负:
正数大于一切负数。
二、隐含条件法:
根据二次根式定义,挖掘隐含条件。
例:比较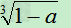 与
与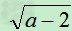 的大小。
的大小。
因为 成立
成立
所以a-2≧0即a≧2
所以1-a≦-1
所以 ≧0,
≧0,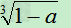 ≦-1
≦-1
所以 >
>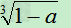
三、同次根式下比较被开方数法:
例:比较4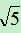 与5
与5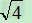 大小
大小
因为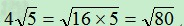
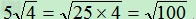
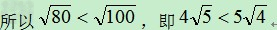
四、作差法:
若a-b>0,则a>b
例:比较3-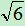 与
与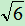 -2的大小
-2的大小
因为3-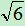 -
-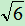 -2
-2
=3-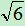 -
-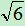 +2
+2
=5-2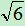
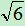 <
< =2.5
=2.5
所以:5-2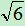 >0
>0
即3-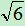 >
>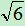 -2
-2
五、作商法:
a>0,b>0,若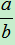 >1,则a>b
>1,则a>b
例:比较 与
与 的大小
的大小
因为 ÷
÷
= ×
×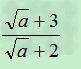
= <1
<1
所以: <
<
六、找中间量法
要证明a>b,可找中间量c,转证a>c,c>b
例:比较 与
与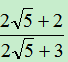 的大小
的大小
因为 >1,1>
>1,1>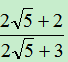
所以 >
>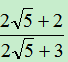
七、平方法:
a>0,b>0,若a2>b2,则a>b。
例:比较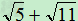 与
与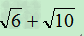 的大小
的大小
(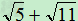 )2=5+2
)2=5+2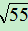 +11=16+2
+11=16+2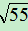
(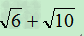 )2=6+2
)2=6+2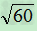 +10=16+2
+10=16+2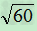
所以: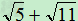 <
<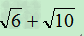
八、倒数法: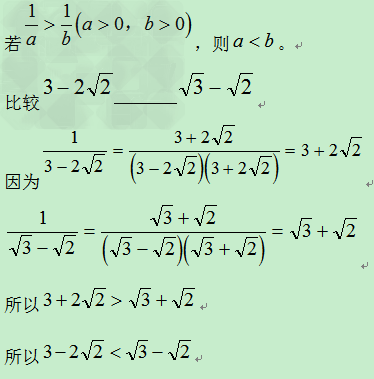
九、有理化法:
可分母有理化,也可分子有理化。 
十、放缩法:
常用无理数口诀记忆:
√2≈1.41421:意思意思而已
√3≈1.7320:一起生鹅蛋
√5≈2.2360679:两鹅生六蛋(送)六妻舅
√7≈2.6457513:二妞是我,气我一生
√8=2√2≈2.82842啊,不啊不是啊
e≈2.718:粮店吃一把
π≈3.14159,26535,897,932,384,262:
山巅一寺一壶酒,尔乐苦杀吾,把酒吃,酒杀尔,杀不死,尔乐尔
有两条边相等的三角形,是等腰三角形,相等的两条边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
等腰三角形的性质:
1.等腰三角形的两个底角度数相等(简写成“等边对等角”)。
2.等腰三角形的顶角的平分线,底边上的中线,底边上的高重合(简写成“等腰三角形的三线合一”)。
3.等腰三角形的两底角的平分线相等(两条腰上的中线相等,两条腰上的高相等)。
4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高(需用等面积法证明)。
7.等腰三角形是轴对称图形,只有一条对称轴,顶角平分线所在的直线是它的对称轴,等边三角形有三条对称轴。
8.等腰三角形中腰的平方等于高的平方加底的一半的平方
9.等腰三角形中腰大于高
10.等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高(需用等面积法证明)
等腰三角形的判定:
1.定义法:在同一三角形中,有两条边相等的三角形是等腰三角形。
2.判定定理:在同一三角形中,有两个角相等的三角形是等腰三角形(简称:等角对等边)。
3.顶角的平分线,底边上的中分线,底边上的高的重合的三角形是等腰三角形。
三角形的三边关系:
在三角形中,任意两边和大于第三边,任意两边差小于第三边。
设三角形三边为a,b,c
则
a+b>c
a+c>b
b+c>a
a-b<c
a-c<b
b-c<a
在直角三角形中,设a、b为直角边,c为斜边。
则两直角边的平方和等于斜边平方。
在等边三角形中,a=b=c
在等腰三角形中, a,b为两腰,则a=b
在三角形ABC的内角A、B、C所对边分别为a、b、c的情况下,c2=a2+b2-2abcosc
三角形的三边关系定理及推论:
(1)三角形三边关系定理:三角形的两边之和大于第三边。
推论:三角形的两边之差小于第三边。
(2)三角形三边关系定理及推论的作用:
①判断三条已知线段能否组成三角形;
②当已知两边时,可确定第三边的范围;
③证明线段不等关系。
与“一个等腰三角形的一边长为1,另一边长为,则等腰三角形的周长...”考查相似的试题有:
- 已知2a-1的算术平方根是3,3a+b-1的平方根是±4,c是13的整数部分,则a+2b-c的平方根为______.
- 如图,△ABC中,点O是AC边上的一个动点,过点O作直线直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F。(1)求...
- 等腰三角形两底角的和是100°,则它的顶角是______°.
- 问题:已知△ABC中,∠BAC=2∠ACB,点D是△ABC内的一点,且AD=CD,BD=BA,探究∠DBC与∠ABC度数的比值,请你完成下列探究过程:先将...
- 如图,AD∥BC,AE∥CD,BD平分∠ABC,求证:AB=CE.
- 如图,在△ABC中,AB=AC,∠ABC=70°,顶点B在直线DE上,且DE∥AC,则∠CBE等于( ) A.40° B.50° C.70° D.80°
- 如图,在△ABC中,AB=AC=25,点D在BC上,AD=24,BD=7,试问AD平分∠BAC吗?为什么?
- 如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,D、E为垂足,BD与CE交于点O,则图中全等三角形共有______对.
- 等腰三角形的一腰上的高为10cm,这条高与底边的夹角为45°,则这个三角形的面积是______.
- 下列三条线段不能构成三角形的是( )A.4cm、2cm、5cmB.13cm、13cm、2cmC.8cm、4cm、3cmD.12cm、10cm、6cm