本试题 “根据表格中的数据可知,下列说法正确的是:( ) 物质的性质物质名称 凝固点/℃ 水 0 水银 -39 酒精 -117 A.水的温度达到0℃就会结冰 B.我国东北地区最低气温...” 主要考查您对凝固的规律及其特点
温度计,体温计的使用及其读数
密度公式的应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 凝固的规律及其特点
- 温度计,体温计的使用及其读数
- 密度公式的应用
晶体凝固时的温度特点:放出热量,温度不变;
非晶体凝固时的温度特点:放出热量,温度不断降低
晶体凝固的条件是:①温度要达到凝固点;②继续向外放热
注意:同种晶体的熔点与凝固点是相同的。
晶体和非晶体凝固时的温度变化曲线(如图所示)
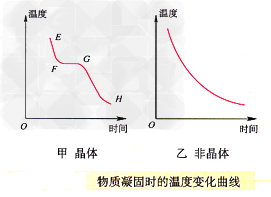
数形结合法在晶体熔化(凝固)过程中的运用
在物理中常采用数学图像方法,把物理现象或物理量之间的关系表示出来。如用温度一时间图像表达物态变化中熔化、凝固、沸腾的特点。涉及的图像有晶体(或非晶体)熔化图像、凝固图像、水的沸腾图像等。图像法具有直观、形象、简捷和概括力强的独特优点。它能将物理情景、物理过程、物理状态以直观的方式呈现在我们面前。
例下表是研究冰熔化时记录的实验数据。
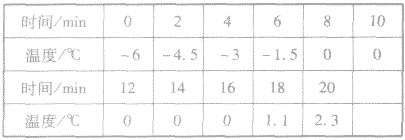
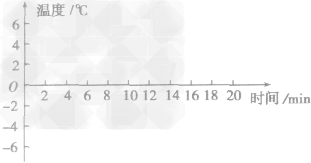
(1)在图中作出冰的熔化图像;
(2)从表中可以看出,冰的熔点是____;
(3)冰熔化过程经历了____min;
(4)从计时开始,经过12mid,冰的温度是____,状态是____。
解析:作图时,步骤是先描点再连线;在8~ 16min时,冰的温度保持0℃不变,故其熔点为0℃;熔化过程经历了8min;由表知,从计时开始,经过12min,冰的温度为0℃,此时冰已持续熔化了4min,但并未熔化完,故为固液共存状态。
答案:(1)冰的熔化图像如图所示
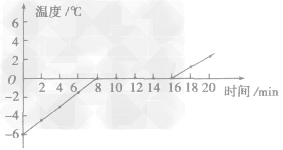
(2)0℃ (3)8 (4)0℃;固液共存状态
图像法描述晶体与非晶体的熔化和凝固过程
非晶体凝固时的温度特点:放出热量,温度不断降低
晶体凝固的条件是:①温度要达到凝固点;②继续向外放热
注意:同种晶体的熔点与凝固点是相同的。
晶体和非晶体凝固时的温度变化曲线(如图所示)

数形结合法在晶体熔化(凝固)过程中的运用
在物理中常采用数学图像方法,把物理现象或物理量之间的关系表示出来。如用温度一时间图像表达物态变化中熔化、凝固、沸腾的特点。涉及的图像有晶体(或非晶体)熔化图像、凝固图像、水的沸腾图像等。图像法具有直观、形象、简捷和概括力强的独特优点。它能将物理情景、物理过程、物理状态以直观的方式呈现在我们面前。
例下表是研究冰熔化时记录的实验数据。


(1)在图中作出冰的熔化图像;
(2)从表中可以看出,冰的熔点是____;
(3)冰熔化过程经历了____min;
(4)从计时开始,经过12mid,冰的温度是____,状态是____。
解析:作图时,步骤是先描点再连线;在8~ 16min时,冰的温度保持0℃不变,故其熔点为0℃;熔化过程经历了8min;由表知,从计时开始,经过12min,冰的温度为0℃,此时冰已持续熔化了4min,但并未熔化完,故为固液共存状态。
答案:(1)冰的熔化图像如图所示

(2)0℃ (3)8 (4)0℃;固液共存状态
图像法描述晶体与非晶体的熔化和凝固过程
| 晶体 | 非晶体 | |
| 物质举例 | 海波、冰、食盐、水晶、明矾、萘、各种金属 | 松香、玻璃、蜂蜡、沥青 |
| 熔点和凝固点 | 有 | 无 |
| 熔化图像 | 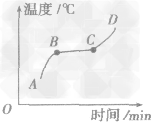 AB段:物质为固态 BC段:熔化过程,物质为固液共存态,吸收热量,温度不变 (此温度为熔点) CD段:物质为液态 |
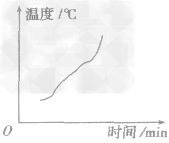 熔化过程中,物质吸收热量,温度逐渐升高 |
| 凝固图像 | EF段:物质为液态 FG段:凝固过程,物质为固液共存态,放出热量,温度不变 (此温度为凝固点) GH段:物质为固态 |
凝固过程中,物质放出热量,温度降低 |
实验室温度计的使用方法:
a.在使用温度计以前,先观察它的量程-能测量的温度范围,然后认清它的分度值
b.温度计的玻璃泡全部浸入被测的液体中,不要碰到容器底或容器壁
c.温度计的玻璃泡浸入被测液体后要稍等一会儿,待温度计的示数稳定后再读数
d.读数时玻璃泡要继续留在被测液体中,视线与温度计中液柱的上表面相平。
体温计的使用方法:
体温计用来测量人体温度。测体温时,玻璃泡内的水银随着温度的升高,发生膨胀,通过细管挤到直管;当体温计离开人体时,水银变冷收缩,细管内的水银断开,直管内的水银不能退回玻璃泡内,所以它表示的仍然是人体的温度。每次使用前,都要拿着体温计把水银甩下去。
体温计,实验室温度计,寒暑表的主要区别:
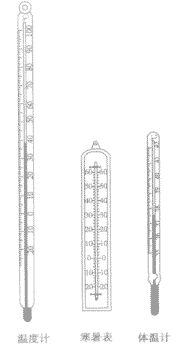
体温计的使用与读数方法
1.明确体温计的量程和分度值。
2.体温计读数时,眼睛通过一条棱看过去,圆弧形的棱相当于一个放大镜,可以观察到放大了的较粗的水银柱,便于观察和读数:
3.用后未甩过的体温计,由于细小缩口的作用,缩口上方的水银柱不能退回玻璃泡。
例:2008年4月,常德市出现了首例“手足口”病例之后,引起了市政府的高度重视,要求各地学校每天对学生进行晨检、晚检、并报告检查情况,其中就用了体温计。图甲是一支常见体温计的示意图,它的量程是____℃,它的分度值为____℃。

由此可知体温计的测量结果比实验用温度计更精确,但因液柱太细难以读数,所以体温计具有特殊构造,其横截面如图乙所示,a为向外凸起的弧形玻璃面,要看清体温计中液柱的位置就应沿_____方向观察(“A”、“B”或“C”),这是利用_______________。
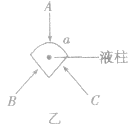
解析:观察题图可知量程和分度值;体温计液柱太细难以读数,利用光学原理放大便于观察,联想放大镜的特征和工作原理,应选从A方向观察。
答案:35~42;0.1;A;凸透镜成正立放大的虚像(或放大镜原理)
不准确温度计的读数方法不准确温度汁的读数可用数学中的比例方法求解:
例:有一支刻度均匀,但实际测量不准确的温度计,把它放在冰水混合物中,示数是4℃;把它放在1 个标准大气压下的沸水中,示数是94℃。把它放在某液体中时,示数是22℃,则该液体的实际温度是____ 。当把该温度计放入实际温度为40℃的温水中时,温度计的示数为____。
解析:根据摄氏温度的规定,冰水混合物的温度是0℃,1个标准大气压下沸水的温度为100℃和已知条件画出的线段图如同所示,按比例计算如下:

解得t1=20℃
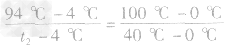
解得t2=40℃

a.在使用温度计以前,先观察它的量程-能测量的温度范围,然后认清它的分度值
b.温度计的玻璃泡全部浸入被测的液体中,不要碰到容器底或容器壁
c.温度计的玻璃泡浸入被测液体后要稍等一会儿,待温度计的示数稳定后再读数
d.读数时玻璃泡要继续留在被测液体中,视线与温度计中液柱的上表面相平。
体温计的使用方法:
体温计用来测量人体温度。测体温时,玻璃泡内的水银随着温度的升高,发生膨胀,通过细管挤到直管;当体温计离开人体时,水银变冷收缩,细管内的水银断开,直管内的水银不能退回玻璃泡内,所以它表示的仍然是人体的温度。每次使用前,都要拿着体温计把水银甩下去。
体温计,实验室温度计,寒暑表的主要区别:
| 实验室温度计 | 体温计 | 寒暑表 | |
| 原理 | 液体的热胀冷缩 | 液体的热胀冷缩 | 液体的热胀冷缩 |
| 玻璃泡内液体 | 水银、煤油、酒精等 | 水银 | 煤油、酒精等 |
| 刻度范围 | -20—110℃ | 35~42℃ | -30—50℃ |
| 分度值 | 1℃ | 0.1℃ | 1℃ |
| 构造 | 玻璃泡上部是均匀细管 | 玻璃泡上部有一段细而弯的“缩口” | 玻璃泡上部是均匀细管 |
| 使用方法 | 不能离开被测物体读数,不能甩 | 可以离开人体读数,使用前要甩几下 | 放在被测环境中直接读数,不能甩 |

体温计的使用与读数方法
1.明确体温计的量程和分度值。
2.体温计读数时,眼睛通过一条棱看过去,圆弧形的棱相当于一个放大镜,可以观察到放大了的较粗的水银柱,便于观察和读数:
3.用后未甩过的体温计,由于细小缩口的作用,缩口上方的水银柱不能退回玻璃泡。
例:2008年4月,常德市出现了首例“手足口”病例之后,引起了市政府的高度重视,要求各地学校每天对学生进行晨检、晚检、并报告检查情况,其中就用了体温计。图甲是一支常见体温计的示意图,它的量程是____℃,它的分度值为____℃。

由此可知体温计的测量结果比实验用温度计更精确,但因液柱太细难以读数,所以体温计具有特殊构造,其横截面如图乙所示,a为向外凸起的弧形玻璃面,要看清体温计中液柱的位置就应沿_____方向观察(“A”、“B”或“C”),这是利用_______________。

解析:观察题图可知量程和分度值;体温计液柱太细难以读数,利用光学原理放大便于观察,联想放大镜的特征和工作原理,应选从A方向观察。
答案:35~42;0.1;A;凸透镜成正立放大的虚像(或放大镜原理)
不准确温度计的读数方法不准确温度汁的读数可用数学中的比例方法求解:
例:有一支刻度均匀,但实际测量不准确的温度计,把它放在冰水混合物中,示数是4℃;把它放在1 个标准大气压下的沸水中,示数是94℃。把它放在某液体中时,示数是22℃,则该液体的实际温度是____ 。当把该温度计放入实际温度为40℃的温水中时,温度计的示数为____。
解析:根据摄氏温度的规定,冰水混合物的温度是0℃,1个标准大气压下沸水的温度为100℃和已知条件画出的线段图如同所示,按比例计算如下:

解得t1=20℃
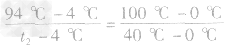
解得t2=40℃

密度公式的应用:
(1)利用m=ρV求质量;利用V=m/ρ求体积
(2)对于密度公式,还要从以下四个方面理解
①同种物质,在一定状态下密度是定值,它不随质量大小或体积大小的改变而改变。当其质量(或体积)增大几倍时,其体积(或质量)也随着增大几倍,而比值是不变的。因此,不能认为物质的密度与质量成正比,与体积成反比;
②具有同种物质的物体,在同一状态下,体积大的质量也大,物体的体积跟它的质量成正比;
③具有不同物质的物体,在体积相同的情况下,密度大的质量也大,物体的质量跟它的密度成正比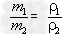 ;
;
④具有不同物质的物体,在质量相同的条件下,密度大的体积反而小,物体的体积跟它的密度成反比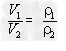 。
。
密度公式的应用:
1. 有关密度的图像问题
此问题一般是给出质量一体积图像,判断或比较物质密度。解答时可在横坐标(或纵坐标)任选一数值,然后在纵坐标(或横坐标)上找到对应的数值,进行分析比较。
例1如图所示,是甲、乙两种物质的m一V图像,由图像可知( )
A.ρ甲>ρ乙
B.ρ甲=ρ乙
C.ρ甲<ρ乙
D.无法确定甲、乙密度的大小
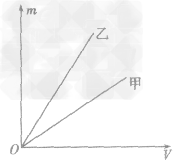
解析:要从图像直接看出甲、乙两种物质的密度大小目前还做不到,我们要先借助图像,根据公式ρ =
 总结规律后方可。
总结规律后方可。如图所示,在横轴上任取一点V0,由V0作横轴的垂线V0B,分别交甲、乙两图线于A、B两点,再分别从A、B两点作纵轴垂线,分别交纵轴于m甲、m乙两点。则甲、乙两种物质的密度分别为
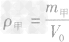 ,ρ乙=
,ρ乙= 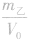 ,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。
,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。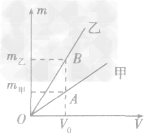
2. 密度公式ρ =
 及变形
及变形 、m=ρV的应用:
、m=ρV的应用:密度的公式是ρ =
 ,可得出质量计算式m=ρV 和体积计算式
,可得出质量计算式m=ρV 和体积计算式 。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。
。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。例2某瓶氧气的密度是5kg/m3,给人供氧用去了氧气质量的一半,则瓶内剩余氧气的密度是_____;容积是10L的瓶子装满了煤油,已知煤油的密度是 0.8×103kg/m3,则瓶内煤油的质量是_____,将煤油倒去4kg后,瓶内剩余煤油的密度是______。
解析:氧气用去一半,剩余部分仍然充满整个氧气瓶,即质量减半体积不变,所以氧气的密度变为 2.5kg/m3。煤油倒去一半后,体积质量同时减半,密度不变。
答案:2.5kg/m3;8kg;0.8×10kg/m3。
3. 比例法求解物质的密度
利用数学的比例式来解决物理问题的方法称之为 “比例法”。能用比例法解答的物理问题具备的条件是:题目所描述的物理现象,由初始状态到终结状态的过程中至少有一个量保持不变,这个不变的量是由初始状态变成终结状态的桥梁,我们称之为“中介量”。
例3甲、乙丽个物体的质量之比为3:2,体积之比为l:3,那么它们的密度之比为( )
A.1:2B.2:1C.2:9D.9:2
解析:(1)写出所求物理量的表达式:
 ,
,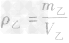
(2)写出该物理量比的表达式:
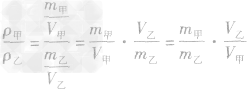
(3)化简:代入已知比值的求解:
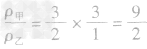
密度、质量、体积计算中的“隐含条件” 问题:
很多物理问题中的有些条件需要仔细审题才能确定,这类条件称为隐含条件。因此寻找隐含条件是解决这类问题的关键。以密度知识为例,密度计算题形式多样,变化灵活,但其中有一些题具有这样的特点:即质量、体积、密度中的某个量在其他量发生变化时保持不变,抓住这一特点,就掌握了求解这类题的规律。
1.隐含体积不变
例1一个瓶子最多能装0.5kg的水,它最多能装_____kg的水银,最多能装_____m3的酒精。 ρ水银=13.6×103kg/m3,ρ水=1.0×103kg/m3,ρ酒精= 0.8×103kg/m3)
解析:最多能装即装满瓶子,由最多装水量可求得瓶子的容积为V=5×10-4m3,则装水银为m水银=13.6×103kg/m3×5×10-4m3=6.8kg。装酒精的体积为瓶子的容积。
答案6.8;5×10-4
2. 隐含密度不变
例2一块石碑的体积为V样=30m3,为测石碑的质量,先取了一块刻制石碑时剔下来的小石块作为样品,其质量是m样=140g,将它放入V1=100cm3的水中后水面升高,总体积增大到V2=150cm3,求这块石碑的质量m碑。
解析:此题中隐含的条件是石碑和样品是同种物质,密度相同,而不同的是它们的体积和质量。依题意可知,样品体积为:
V样=V2-V1=150cm3一100cm3=50cm3 =5.0×10-5m3
得
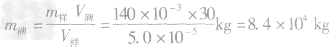 =84t
=84t答案:84t
3. 隐含质量不变
例3质量为450g的水结成冰后,其体积变化了 ____m3。(ρ水=0.9×103kg/m3)
解析:水结成冰后,密度减小,450g水的体积为
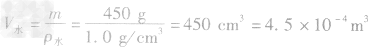 ,水结成冰后,质量不变,因此冰的体积为
,水结成冰后,质量不变,因此冰的体积为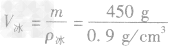 =500cm3=5.0×10-4m3,
=500cm3=5.0×10-4m3,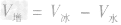 =5.0× 10-4m3一4.5×10-4m3=5×10-5m3。
=5.0× 10-4m3一4.5×10-4m3=5×10-5m3。合金物体密度的相关计算:
首先要抓住合金体的总质量与总体积分别等于各种物质的质量之和与体积之和这一特征,然后根据具体问题,灵活求解。
例两种不同的金属,密度分别为ρ1、ρ2:
(1)若墩质量相等的金属混合后制成合金,则合金的密度为____。
(2)若取体积相等的金属混合后制成合金,则合金的密度为_____。
解析:这道题的关键是抓住“两总”不变,即总质量和总体积不变。在(1)中,两种金属的质量相等,设为m1=m2=m,合金的质量m总=2m,则密度为ρ1的金属的体积V1=
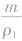 ,密度为ρ2的金属的体积V2=
,密度为ρ2的金属的体积V2=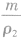 ,合金的体积
,合金的体积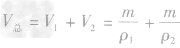 ,则合金的密度
,则合金的密度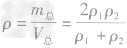
在(2)中两种金属的体积相等,设为
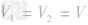 ,合金的体积
,合金的体积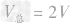 ,密度为ρ1的金属的质量m1=
,密度为ρ1的金属的质量m1=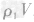 ,密度为ρ2的金属的质量为
,密度为ρ2的金属的质量为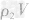 ,合金的质量m总
,合金的质量m总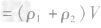 ,合金的密度为
,合金的密度为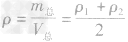 。
。答案:

注意:上述规律也适用于两种液体的混合,只要混合液的总质量和总体积不变即可。
发现相似题
与“根据表格中的数据可知,下列说法正确的是:( ) 物质的性质...”考查相似的试题有:
- 在我国北方很冷的地区要使用酒精温度计,而不使用水银温度计,这是因为[ ]A.液态水银比液态酒精的凝固点高B.水银是热的不良...
- 北方冬天的地窖放几桶水,可以利用水_______时要____________,使地窖内的温度不会降的过低而冻坏地窖内存放的菜。
- 在下列测量中,A 物体的长度为________cm ;温度计的示数为___________℃。
- 有一种纪念币,它的质量是16克,把它放入一盛满水的量筒中,测得溢出的水的质量为2克。求:(1)该纪念币的体积;(2)制作该...
- 一个小瓶装满水时质量为32g,装满酒精时质量为28g,则这个小瓶的质量和容积各是多大?(ρ酒精=0.8×103kg/m3)
- 在建设资源节约型社会里,武汉光谷已经使用风光互补路灯系统(如图所示).风光互补路灯系统具备了风能和太阳能产品的双重优...
- 为制作高度为2m的英雄塑像,先用同样材料精制一个小样品,高度为20cm,质量为3kg,那么这个塑像的质量将是______kg.
- 小明同学在课外活动课中,想测出一个油罐内油的质量,已经知道这个油罐的容积是50m3,他取出一些样品,测出20cm3这种油的质量...
- 一块冰融化成水,状态变了,质量______,体积______,密度______.(填“变大”、“变小”或“不变”)
- 甲、乙两实心球,质量比为3:2,密度比为1:3,则其体积比为______.