本试题 “如图,一个简单组合体的正视图和侧视图都是由一个正方形与一个正三角形构成的相同的图形,俯视图是一个半径为的圆(包括圆心).则该组合体的表面积等于[ ]A...” 主要考查您对空间几何体的三视图
柱体、椎体、台体的表面积与体积
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 空间几何体的三视图
- 柱体、椎体、台体的表面积与体积
中心投影:
光由一点向外散射形成的投影叫做中心投影,其投影的大小随物体与投影中心间距离的变化而变化。
平行投影:
在一束平行光线照射下形成的投影叫做平行投影。在平行投影中,投影线正对着投影面时,叫做正投影,否则叫做斜投影。
空间几何体的三视图:
光线从几何体的前面向后面正投影,得到投影图,叫做几何体的正视图;光线从几何体的左面向右面正投影,得到投影图,叫做几何体的侧视图;从几何体的上面向下面正投影,得到投影图,叫做几何体的俯视图。几何体的正视图、侧视图、俯视图统称为几何体的三视图。
注:正视图反映了物体上下、左右的位置关系,即反映了物体的高度和长度;
俯视图反映了物体左右、前后的位置关系,即反映了物体的长度和宽度;
侧视图反映了物体上下、前后的位置关系,即反映了物体的高度和宽度。
平行投影与中心投影的区别和联系:
①平行投影的投射线都互相平行,中心投影的投射线是由同一个点发出的.如图所示,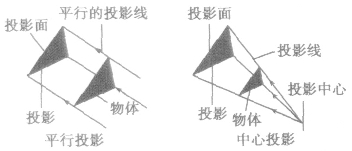
②平行投影是对物体投影后得到与物体等大小、等形状的投影;中心投影是对物体投影后得到比原物体大的、形状与原物体的正投影相似的投影.
③中心投影和平行投影都是空间图形的基本画法,平行投影包括斜二测画法和三视图.中心投影后的图形与原图形相比虽然改变较多,但直观性强,看起来与人的视觉效果一致,最像原来的物体.
④画实际效果图时,一般用中心投影法,画立体几何中的图形时一般用平行投影法.
画三视图的规则:
①画三视图的规则是正侧一样高,正俯一样长,俯侧一样宽.即正视图、侧视图一样高,正视图、俯视图一样长,俯视图、侧视图一样宽;
②画三视图时应注意:被挡住的轮廓线画成虚线,能看见的轮廓线和棱用实线表示,不能看见的轮廓线和棱用虚线表示,尺寸线用细实线标出;D表示直径,R表示半径;单位不注明时按mm计;
③对于简单的几何体,如一块砖,向两个互相垂直的平面作正投影,就能真实地反映它的大小和形状.一般只画出它的正视图和俯视图(二视图).对于复杂的几何体,三视图可能还不足以反映它的大小和形状,还需要更多的投射平面.
常见几何体的三视图:
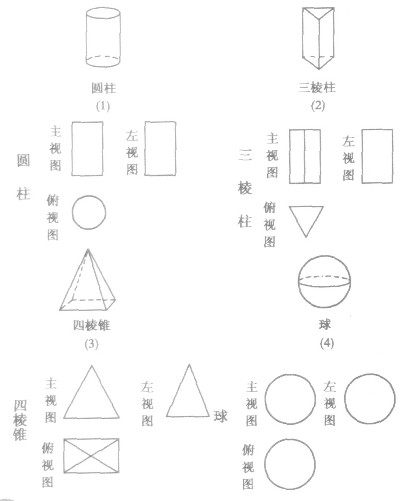
侧面积和全面积的定义:
(1)侧面积的定义:把柱、锥、台的侧面沿着它们的一条侧棱或母线剪开,所得到的展开图的面积,就是空间几何体的侧面积.
(2)全面积的定义:空间几何体的侧面积与底面积的和叫做空间几何体的全面积,
柱体、锥体、台体的表面积公式(c为底面周长,h为高,h′为斜高,l为母线)
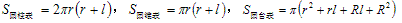
柱体、锥体、台体的体积公式:

多面体的侧面积与体积:
| 多面体 | 图像 | 侧面积 | 体积 |
| 棱柱 |
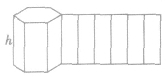 |
直棱柱的侧面展开图是矩形 |
 |
| 棱锥 |
 |
正棱柱的侧面展开图是一些全等的等腰三角形,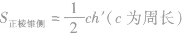 |
 |
| 棱台 |
 |
正棱台的侧面展开图是一些全等的等腰梯形,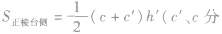  |
 |
旋转体的侧面积和体积:
| 旋转体 | 图形 | 侧面积与全面积 | 体积 |
| 圆柱 |
 |
圆柱的侧面展开图的矩形: |
 |
| 圆锥 |
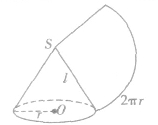 |
圆锥的侧面展开图是扇形: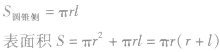 |
 |
| 圆台 |
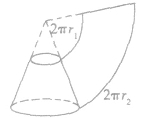 |
圆台的侧面展开图是扇环: |
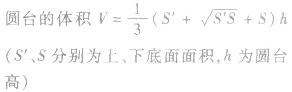 |
| 球 |
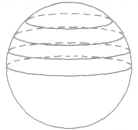 |
 |
 |
与“如图,一个简单组合体的正视图和侧视图都是由一个正方形与一...”考查相似的试题有:
- 如图,是一个几何体的三视图,则此三视图所描述几何体的表面积为( )A.1+2B.2+2C.3+2D.52+2
- 若某几何体的正视图为下图(1),则此几何体的俯视图不可能是 A) B) C) D)
- 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形,则用( )个这样的几何体可以拼成一个...
- 如图,正方体ABCD-A'B'C'D'中,M,E是AB的三等分点,G,N是CD的三等分点,F,H分别是BC,MN的中点,则四棱锥A'-EFGH的侧视图为( )
- 已知△ABC的平面直观图△A′B′C′是边长为a的正三角形,那么原△ABC的面积为____________.
- 一空间几何体的三视图如图所示,则该几何体的体积为______.
- 已知如图是一个空间几何体的三视图,则该几何体的表面积为______.
- 一个几何体的三视图如图所示(单位长度:),俯视图中圆与四边形相切,且该几何体的体积为,则该几何体的高为 .
- 如图为一几何体的三视图,则该几何体体积为( )A.B.6C.D.
- 如图,正三棱台的上、下两底边长之比为,连接,把正三棱台分成三个三棱锥,求这三个三棱锥的体积之比.