本试题 “已知向量a=(3,0),b=(0,1),若a-λb与2a+b共线,则实数λ的值为A.1B.-1C.D.-” 主要考查您对向量共线的充要条件及坐标表示
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 向量共线的充要条件及坐标表示
向量共线的充要条件:
向量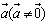 与
与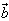 共线,当且仅当有唯一一个实数λ,使得
共线,当且仅当有唯一一个实数λ,使得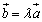 。
。
向量共线的几何表示:
设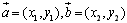 ,其中
,其中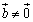 ,当且仅当
,当且仅当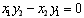 时,向量
时,向量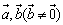 共线。
共线。
向量共线(平行)基本定理的理解:
(1)对于向量a(a≠0),b,如果有一个实数λ,使得b=λa,那么由向量数乘的定义知,a与b共线.
(2)反过来,已知向量a与b共线,a≠0,且向量b的长度是向量a的长度的μ倍,即|b|=μ|a|,那么当a与b同方向时,有b=μa;当a与b反方向时,有b=-μa.
(3)向量平行与直线平行是有区别的,直线平行不包括重合.
(4)判断a(a≠0)与b是否共线时,关键是寻找a前面的系数,如果系数有且只有一个,说明共线;如果找不到满足条件的系数,则这两个向量不共线.
(5)如果a=b=0,则数λ仍然存在,且此时λ并不唯一,是任意数值.
发现相似题
与“已知向量a=(3,0),b=(0,1),若a-λb与2a+b共线,则实数λ的值...”考查相似的试题有:
- 在四边形ABCD中,,且=0,则四边形ABCD是( )A.矩形B.菱形C.直角梯形D.等腰梯形
- 椭圆的中心是原点O,它的短轴长为,相应于焦点F(c,0)(c>0)的准线l与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交...
- 设F1,F2分别为椭圆C:(a>b>0)的左、右焦点,过F2的直线l与椭圆C相交于A、B两点,直线l的倾斜角为60°,F1到直线l的距离为...
- 设P,Q为△ABC内的两点,且AP=mAB+nAC (m,n>0)AQ=pAB+qAC (p,q>0),则△ABP的面积与△ABQ的面积之比为______.
- 在平面直角坐标系中,O为坐标原点,设向量,其中,若,C点所有可能的位置区域用阴影表示正确的是[ ]A.B.C.D.
- 设过点P(x,y)的直线分别与x轴的正半轴和y轴的正半轴交于A、B两点,若,且,则点P的轨迹方程是( )A.B.C.D.
- 若对n个向量a1•a2,…an存在n个不全为零的实数k1,k2,…,kn,使得k1a1+k2a2+…,knan=成立,则称向量a1、a2,…an为“线性相关”...
- 在四边形ABCD中,,且,则四边形ABCD是( )A.矩形B.菱形C.直角梯形D.等腰梯形
- 已知点A(1,2,1),B(-1,3,4),D(1,1,1),若AP=2PB,则|PD|的值是______.
- 如图,两块斜边长相等的直角三角板在一起,若,则x=( ),y=( )。