返回

高中数学

首页
首页 高中数学知识 复数相等的充要条件 复数的四则运算 试题正文
  • 填空题
    若复数z满足iz=2+3i（i是虚数单位），则z=______．
    本题信息：数学填空题难度一般 来源:未知
  • 本题答案
    查看答案
本试题 “若复数z满足iz=2+3i（i是虚数单位），则z=______．” 主要考查您对

复数相等的充要条件

复数的四则运算

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 复数相等的充要条件
  • 复数的四则运算

两个复数相等的定义：

如果两个复数的实部和虚部分别相等，那么我们就说这两个复数相等，即：如果a，b，c，d∈R，那么a+bi=c+dia=c，b=d。特殊地，a，b∈R时，a+bi=0a=0，b=0.
复数相等的充要条件，提供了将复数问题化归为实数问题解决的途径。


复数相等特别提醒：

一般地，两个复数只能说相等或不相等，而不能比较大小。如果两个复数都是实数，就可以比较大小，也只有当两个复数全是实数时才能比较大小。

解复数相等问题的方法步骤：

（1）把给的复数化成复数的标准形式；
（2）根据复数相等的充要条件解之。


复数的运算：

1、复数z1与z2的和的定义：z1+z2=（a+bi）+（c+di）=（a+c）+（b+d）i；
2、复数z1与z2的差的定义：z1-z2=（a+bi）-（c+di）=（a-c）+（b-d）i；
3、复数的乘法运算规则：设z1=a+bi，z2=c+di（a、b、c、d∈R）是任意两个复数，那么它们的积（a+bi）（c+di）=（ac-bd）+（bc+ad）i，其实就是把两个复数相乘，类似两个多项式相乘，在所得的结果中把i2换成-1，并且把实部与虚部分别合并，两个复数的积仍然是一个复数。
4、复数的除法运算规则：。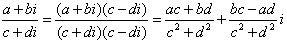

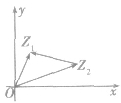
复数加法的几何意义：

设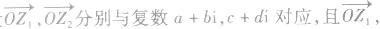 为邻边画平行四边形就是复数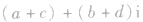对应的向量。

复数减法的几何意义：
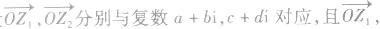
复数减法是加法的逆运算，设，则这两个复数的差对应，这就是复数减法的几何意义。
 
共轭复数：

当两个复数的实部相等，虚部互为相反数时，这两个复数叫做互为共轭复数。
虚部不等于0的两个共轭复数也叫做共轭虚数。
复数z=a+bi和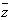=a-bi（a、b∈R）互为共轭复数。


复数的运算律：

1、复数的加法运算满足交换律：z1+z2=z2+z1；
结合律：（z1+z2）+z3=z1+（z2+z3）；
2、减法同加法一样满足交换律、结合律。
3、乘法运算律：（1）z1（z2z3）=（z1z2）z3；（2）z1（z2+z3）=z1z2+z1z3；（3）z1（z2+z3）=z1z2+z1z3


共轭复数的性质：


 
 

发现相似题
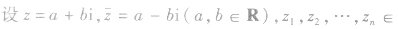
与“若复数z满足iz=2+3i（i是虚数单位），则z=______．”考查相似的试题有：