己知f（x）在（-1，1）上有定义，f（12）=-1，且满足x．，y∈（-1，1）有f（x）+f（y）=f(x+y1-xy)．（I）判断为f,高中,数学试题,函数的奇偶性、周期性考点,好技网

解答题
己知f（x）在（-1，1）上有定义，f（
1
2
）=-1，且满足x．，y∈（-1，1）有f（x）+f（y）=f(
x+y
1-xy
)．
（I）判断为f（x）在（-1，1）上的奇偶性：
（II）对数列x₁=
1
2
，x_n+1=
2xn
1+xn2
，求f（x_n）
（111）求证：
1
f(x1)
+
1
fx2)
+…+
1
f(xn)
＞-
2n+5
n+2
．

本题信息：数学解答题难度一般来源:未知
本题答案
查看答案

本试题 “己知f（x）在（-1，1）上有定义，f（12）=-1，且满足x．，y∈（-1，1）有f（x）+f（y）=f(x+y1-xy)．（I）判断为f（x）在（-1，1）上的奇偶性：（II）对数列x1...” 主要考查您对
函数的奇偶性、周期性
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。

函数的奇偶性、周期性

函数的奇偶性定义：

偶函数：一般地，如果对于函数f（x）的定义域内任意一个x，都有f（-x）=f（x），则称函数f（x）为偶函数。
奇函数：一般地，如果对于函数f（x）的定义域内任意一个x，都有f（-x）＝-f（x），那么函数f（x）是奇函数。

函数的周期性：

（1）定义：若T为非零常数，对于定义域内的任一x，使f（x+T）=f（x）恒成立，则f（x）叫做周期函数，T叫做这个函数的一个周期。
周期函数定义域必是无界的。
（2）若T是周期，则k·T（k≠0，k∈Z）也是周期，所有周期中最小的正数叫最小正周期。一般所说的周期是指函数的最小正周期。
周期函数并非都有最小正周期，如常函数f（x）=C。

奇函数与偶函数性质：

（1）奇函数与偶函数的图像的对称性：奇函数的图像关于原点对称，偶函数的图像关于y轴对称。
（3）在公共定义域内，①两个奇函数的和是奇函数，两个奇函数的积是偶函数； ②两个偶函数的和、积是偶函数； ③一个奇函数，一个偶函数的积是奇函数。

注：定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件．

1、函数是奇函数或偶函数的前提定义域必须关于原点对称；定义域在数轴上关于原点对称是函数f(x)为奇函数或偶函数的必要但不充分条件．

2、函数的周期性令a , b 均不为零，若：
（1）函数y = f(x) 存在 f(x)=f(x + a) ==> 函数最小正周期 T=|a|
（2）函数y = f(x) 存在f(a + x) = f(b + x) ==> 函数最小正周期 T=|b-a|
（3）函数y = f(x) 存在 f(x) = -f(x + a) ==> 函数最小正周期 T=|2a|
（4）函数y = f(x) 存在 f(x + a) = ==> 函数最小正周期 T=|2a|
（5）函数y = f(x) 存在 f(x + a) = 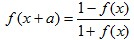==> 函数最小正周期 T=|4a|

发现相似题

与“己知f（x）在（-1，1）上有定义，f（12）=-1，且满足x．，y∈...”考查相似的试题有：