本试题 “下列各式计算正确的是( )A.m8÷m4=m2B.a2•a3=a6C.1x+1y=2x+yD.6÷2=3” 主要考查您对有理数除法
有理数的乘方
分式的加减
二次根式的乘除
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 有理数除法
- 有理数的乘方
- 分式的加减
- 二次根式的乘除
有理数除法定义:
已知两个因数的积与其中一个因数,求另一个因数的运算叫做有理数的除法。
有理数除法注意:
①0不能做除数;
②有理数的除法和乘法是互逆运算;
③在做除法运算时,根据同号得正,异号的负的法则先确定符号,在把绝对值相除,若在算式中有带分数,一般化成假分数进行计算,若不能整除,则除法运算都转化为乘法运算。
已知两个因数的积与其中一个因数,求另一个因数的运算叫做有理数的除法。
有理数的除法法则:
(1)除以一个数,等于乘上这个数的倒数;
(2)两个数相除,同号得正,异号得负,并把绝对值相除;
(3)0除以任何一个不等于0的数都等于0。
有理数除法注意:
①0不能做除数;
②有理数的除法和乘法是互逆运算;
③在做除法运算时,根据同号得正,异号的负的法则先确定符号,在把绝对值相除,若在算式中有带分数,一般化成假分数进行计算,若不能整除,则除法运算都转化为乘法运算。
有理数乘方的定义:
求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂。在an中,a叫做底数,n叫做指数。
22、73也可以看做是乘方运算的结果,这时它们表示数,分别读作“2的2次幂”、“7的3次幂”,其中2、7叫做底数,6、3叫做指数。
①习惯上把22叫做2的平方,把23叫做2的立方;
②当底数是负数或分数时,要先用括号将底数括上,再在其右上角写指数,指数要写得小些。
乘方的性质:
乘方是乘法的特例,其性质如下:
(1)正数的任何次幂都是正数;
(2)负数的偶次幂是正数,负数的奇次幂是负数;
(3)0的任何(除0以外)次幂都是0;
(4)a2是一个非负数,即a2≥0。
有理数乘方法则:
①负数的奇次幂是负数,负数的偶次幂是正数。例如:(-2)3=-8,(-2)2=4
②正数的任何次幂都是正数,0的任何正整数次幂都是0.例如:22=4,23=8,03=0
点拨:
①0的次幂没意义;
②任何有理数的偶次幂都是非负数;
③由于乘方是乘法的特例,因此有理数的乘方运算可以用有理数的乘法运算完成;
④负数的乘方与乘方的相反数不同。
乘方示意图:

求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂。在an中,a叫做底数,n叫做指数。
22、73也可以看做是乘方运算的结果,这时它们表示数,分别读作“2的2次幂”、“7的3次幂”,其中2、7叫做底数,6、3叫做指数。
①习惯上把22叫做2的平方,把23叫做2的立方;
②当底数是负数或分数时,要先用括号将底数括上,再在其右上角写指数,指数要写得小些。
乘方的性质:
乘方是乘法的特例,其性质如下:
(1)正数的任何次幂都是正数;
(2)负数的偶次幂是正数,负数的奇次幂是负数;
(3)0的任何(除0以外)次幂都是0;
(4)a2是一个非负数,即a2≥0。
有理数乘方法则:
①负数的奇次幂是负数,负数的偶次幂是正数。例如:(-2)3=-8,(-2)2=4
②正数的任何次幂都是正数,0的任何正整数次幂都是0.例如:22=4,23=8,03=0
点拨:
①0的次幂没意义;
②任何有理数的偶次幂都是非负数;
③由于乘方是乘法的特例,因此有理数的乘方运算可以用有理数的乘法运算完成;
④负数的乘方与乘方的相反数不同。
乘方示意图:

分式的加减法则:
同分母的分式相加减,分母不变,把分子相加减;
异分母的分式相加减,先通分,变为同分母分式,然后再加减。
用式子表示为: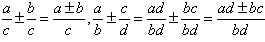
分式的加减要求:
①分式的加减运算结果必须是最简分式或整式,运算中要适时地约分;
②如果一个分式与一个整式相加减,那么可以把整式看成是分母为1的分式,先通分,再进行加减。
同分母的分式相加减,分母不变,把分子相加减;
异分母的分式相加减,先通分,变为同分母分式,然后再加减。
用式子表示为:
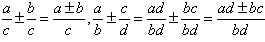
分式的加减要求:
①分式的加减运算结果必须是最简分式或整式,运算中要适时地约分;
②如果一个分式与一个整式相加减,那么可以把整式看成是分母为1的分式,先通分,再进行加减。
二次根式的乘除法则:
1、二次根式的乘法原则: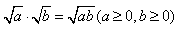 ,即两个二次根式相乘,根指数不变,相乘的结果是一个二次根式或有理式。
,即两个二次根式相乘,根指数不变,相乘的结果是一个二次根式或有理式。
2、二次根式的除法原则: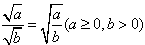 ,即二次根式相除,就是把被被开方数相除,根指数不变。
,即二次根式相除,就是把被被开方数相除,根指数不变。
有理化根式:如果两个含有根式的代数式的积不再含有根式,那么这两个代数式叫做有理化根式,也称有理化因式。
1、二次根式的乘法原则:
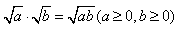 ,即两个二次根式相乘,根指数不变,相乘的结果是一个二次根式或有理式。
,即两个二次根式相乘,根指数不变,相乘的结果是一个二次根式或有理式。 2、二次根式的除法原则:
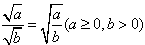 ,即二次根式相除,就是把被被开方数相除,根指数不变。
,即二次根式相除,就是把被被开方数相除,根指数不变。 有理化根式:如果两个含有根式的代数式的积不再含有根式,那么这两个代数式叫做有理化根式,也称有理化因式。
发现相似题
与“下列各式计算正确的是( )A.m8÷m4=m2B.a2•a3=a6C.1x+1y=2...”考查相似的试题有:
- 用科学记数法表示0.0000023=
- 下列计算正确的是( )A.a•a3=a2B.a+a2=a3C.(a3)2=a5D.a2÷a2=1
- 31000的末位数是( )。
- 计算23+(-2)3的值是[ ]A、0B、12C、16D、18
- 下列计算正确的是( )A.2a2+3a3=5a5B.a8a4=a2C.(-2a3)3=-6a9D.(13)3=127
- 把一张厚度为0.1mm的纸连续对折8次后,其厚度接近于[ ]A.0.8mmB.2.5mmC.2.5cmD.0.8cm
- 已知,且,求的值
- (﹣2)6读作:_______,其中底数是_________,指数是_________,(﹣2)6是_________(填正或负).
- 已知|m﹣2|+(n+1)2=0,则m+n=_________.
- 化简: