本试题 “经市场调查,某旅游城市在过去的一个月内(以30天计),日旅游人数f(t)(万人)与时间t(天)的函数关系近似满足,人均消费g(t)(元)与时间t(天)的函...” 主要考查您对分段函数与抽象函数
基本不等式及其应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 分段函数与抽象函数
- 基本不等式及其应用
分段函数:
1、分段函数:定义域中各段的x与y的对应法则不同,函数式是分两段或几段给出的;
分段函数是一个函数,定义域、值域都是各段的并集。
抽象函数:
我们把没有给出具体解析式的函数称为抽象函数;
一般形式为y=f(x),或许还附有定义域、值域等,如:y=f(x),(x>0,y>0)。
知识点拨:
1、绝对值函数去掉绝对符号后就是分段函数。
2、分段函数中的问题一般是求解析式、反函数、值域或最值,讨论奇偶性单调性等。
3、分段函数的处理方法:分段函数分段研究。
基本不等式:
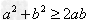 (当且仅当a=b时取“=”号);
(当且仅当a=b时取“=”号);
变式:①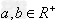 ,
,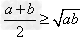 (当且仅当a=b时取“=”号),即两个正数的算术平均不小于它们的几何平均。
(当且仅当a=b时取“=”号),即两个正数的算术平均不小于它们的几何平均。
②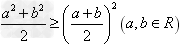 ;③
;③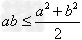 ;④
;④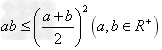 ;
;
对基本不等式的理解:
(1)基本不等式的证明是利用重要不等式推导的,即 ,即有
,即有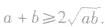
(2)基本不等式又称为均值定理、均值不等式等,其中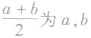 的算术平均数,
的算术平均数,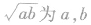 的几何平均数,本定理也可叙述为:两个正数的算术平均数不小于它们的几何平均数.
的几何平均数,本定理也可叙述为:两个正数的算术平均数不小于它们的几何平均数.
(3)要特别注意不等式成立的条件和等号成立的条件.均值不等式中:①当a=b时取等号,即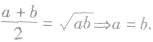
对于两个正数x,y,若已知xy,x+y,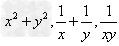 中的某一个为定值,可求出其余各个的最值:
中的某一个为定值,可求出其余各个的最值:
如:(1)当xy=P(定值),那么当x=y时,和x+y有最小值2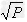 ,
,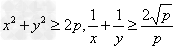 ;
;
(2)x+y=S(定值),那么当x=y时,积xy有最大值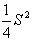 ,
,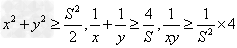 ;
;
(3)已知x2+y2=p,则x+y有最大值为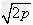 ,
, 。
。
应用基本的不等式解题时:
注意创设一个应用基本不等式的情境及使等号成立的条件,即“一正、二定、三相等”。
利用基本不等式比较实数大小:
(1)注意均值不等式的前提条件.
(2)通过加减项的方法配凑成使用均值定理的形式.
(3)注意“1”的代换.
(4)灵活变换基本不等式的形式,并注重其变形形式的运用.重要不等式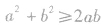 的形式可以是
的形式可以是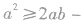
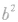 ,也可以是
,也可以是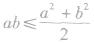 ,还可以是
,还可以是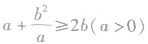 等,不仅要掌握原来的形式,还要掌握它的几种变形形式以及公式的逆用等,以便应用.
等,不仅要掌握原来的形式,还要掌握它的几种变形形式以及公式的逆用等,以便应用.
(5)合理配组,反复应用均值不等式。

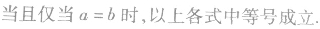
与“经市场调查,某旅游城市在过去的一个月内(以30天计),日旅...”考查相似的试题有:
- 已知函数(1)画出函数f(x)的简图;(2)求f(f(2))的值。
- 已知定义在R上的函数f(x)在[0,+∞)上单调递增,且对任意的x,y∈R都有f(x+y)=f(x)+f(y).若f(3x)+f(9x-2)>0,则...
- 已知函数,则( )A.4 B. C.-4 D-
- 定义函数f(x)=2cosx,(sinx<cosx)2sinx (sinx≥cosx),给出下列四个命题:①该函数的值域是[-2,2];②该函数是以π为最小正周期...
- 已知函数f(x)=x2+ax+7+ax+1,a∈R.若对于任意的x∈N*,f (x)≥4恒成立,则a的取值范围是______.
- 设a>b,c>d,则下列不等式恒成立的是[ ]A.a﹣c>b﹣dB.ac>bdC.D.b+d<a+c
- 下面四个不等式(1)≥ (2)≤ (3)≥2 (4)≥其中恒成立的有( )A.1个B.2个C.3个D.4个
- 若a>3,则的最小值是( )。
- 已知直线x+2y=2与x轴,y轴分别交于A,B两点,若动点P(a,b)在线段AB上,则ab的最大值为( )A.12B.2C.3D.13
- 已知x>0,y>0,9x+y=xy,则x+y的最小值为( )。