本试题 “问题提出:以n边形的n个顶点和它内部的m个点,共(m+n)个点作为顶点,可把原n边形分割成多少个互不重叠的小三角形?问题探究:为了解决上面的问题,我们将采...” 主要考查您对多边形的内角和和外角和
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 多边形的内角和和外角和
在平面内,由若干不在同一直线上的线段首尾顺次连接组成的封闭图形叫做多边形。
对角线:在多边形中,连接不相邻的两个顶点的线段叫做多边形的对角线。
外角:多边形的一边与另一边的反向延长线所组成的角叫做这个多边形的外角。
如图示:
多边形的内角和:
n边形的内角和等于(n-2)·180°。(多边形内角和定理)
多边形的外角和:
在多边形的每个顶点处取多边形的一个外角,它们的和叫做多边形的外角和。
多边形的外角和等于360°。(与边数无关) (多边形的外角和定理)
多边形外角和列举: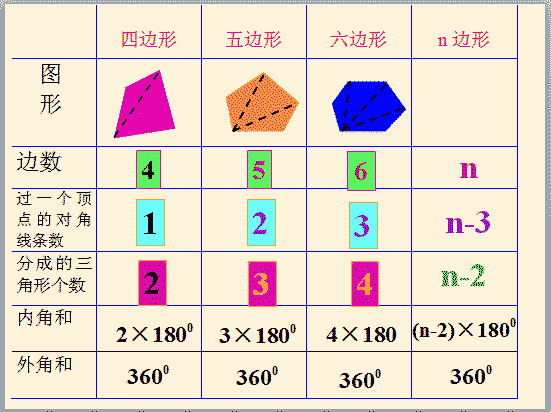
发现相似题
与“问题提出:以n边形的n个顶点和它内部的m个点,共(m+n)个点...”考查相似的试题有:
- 如图,∠1、∠2、∠3、∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=70°,则∠AED的度数是[ ]A.110°B.108°C.105°D.100°
- 已知一个多边形的内角和是540°,则这个多边形是( )A.四边形B.五边形C.六边形D.七边形
- 多边形的内角中,锐角的个数最多有( )A.1个B.2个C.3个D.4个
- 如图,∠A+∠ABC+∠C+∠D+∠E+∠F=( )度.
- 一个正多边形,它的一个外角等于与它相邻的内角的,则这个多边形是( )边形。
- 已知任意三角形的内角和为180°,试利用多边形中过某一点的对角线条数,寻求多边形内角和的公式。根据上图所示,一个四边形可...
- 九边形的外角和为______°.
- 在四边形ABCD中,∠B=60°,∠A是∠C的2倍, ∠D=90°,求∠A和∠C的度数。
- 已知一个n边形的外角和是内角和的27,则边数n=______.
- 如图,小亮从A点出发前10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了( )m.