本试题 “我们知道任何实数的平方一定是一个非负数,即:(a+b)2≥0,且-(a+b)2≤0。据此,我们可以得到下面的推理:∵x2+2x+3=(x2+2x+1)+2=(x+1)2+2,而(x+1)2≥...” 主要考查您对二次函数的最大值和最小值
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 二次函数的最大值和最小值
二次函数的最值:
1.如果自变量的取值范围是全体实数,则当a>0时,抛物线开口向上,有最低点,那么函数在 处取得最小值y最小值=
处取得最小值y最小值= ;
;
当a<0时,抛物线开口向下,有最高点,即当 时,函数取得最大值,y最大值=
时,函数取得最大值,y最大值= 。
。
也即是:如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当 时,
时,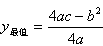 。
。
2.如果自变量的取值范围是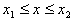 ,那么,首先要看
,那么,首先要看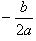 是否在自变量取值范围
是否在自变量取值范围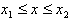 内,若在此范围内,则当x=
内,若在此范围内,则当x=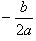 时,
时,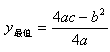 ;若不在此范围内,则需要考虑函数在
;若不在此范围内,则需要考虑函数在 范围内的增减性,如果在此范围内,y随x的增大而增大,则当x=x2 时,
范围内的增减性,如果在此范围内,y随x的增大而增大,则当x=x2 时,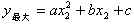 ,当x=x1 时
,当x=x1 时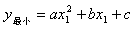 ;如果在此范围内,y随x的增大而减小,则当x=x1时,
;如果在此范围内,y随x的增大而减小,则当x=x1时, ,当x=x2时
,当x=x2时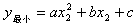 。
。
1.如果自变量的取值范围是全体实数,则当a>0时,抛物线开口向上,有最低点,那么函数在
 处取得最小值y最小值=
处取得最小值y最小值= ;
;当a<0时,抛物线开口向下,有最高点,即当
 时,函数取得最大值,y最大值=
时,函数取得最大值,y最大值= 。
。 也即是:如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当
 时,
时,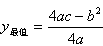 。
。2.如果自变量的取值范围是
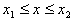 ,那么,首先要看
,那么,首先要看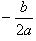 是否在自变量取值范围
是否在自变量取值范围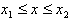 内,若在此范围内,则当x=
内,若在此范围内,则当x=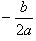 时,
时,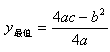 ;若不在此范围内,则需要考虑函数在
;若不在此范围内,则需要考虑函数在 范围内的增减性,如果在此范围内,y随x的增大而增大,则当x=x2 时,
范围内的增减性,如果在此范围内,y随x的增大而增大,则当x=x2 时,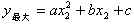 ,当x=x1 时
,当x=x1 时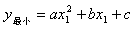 ;如果在此范围内,y随x的增大而减小,则当x=x1时,
;如果在此范围内,y随x的增大而减小,则当x=x1时, ,当x=x2时
,当x=x2时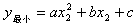 。
。 发现相似题
与“我们知道任何实数的平方一定是一个非负数,即:(a+b)2≥0,...”考查相似的试题有:
- 如图,抛物线与轴交于(,0)、(,0)两点,且,与轴交于点,其中是方程的两个根。(1)求抛物线的解析式;(2)点是线段上...
- 二次函数的图象如图所示,则下列关系式错误的是( )A.B.C.D.
- 已知一元二次方程x2+ax+a-2=0.(1)求证:不论a为何实数,此方程总有两个不相等的实数根;(2)设a<0,当二次函数y=x2...
- 如图,在平面直角坐标系中,矩形OABC的顶点A(0,3),C(,0).将矩形OABC绕原点顺时针旋转90°,得到矩形.设直线与轴交于...
- (11·贺州)函数y=ax-2 (a≠0)与y=ax2(a≠0)在同一平面直角坐标系中的图象可能是
- 当m在可取值范围内取不同的值时,代数式的最小值是( ) A.0 B.5 C.3 D.9
- 如图:在平面直角坐标系中,将长方形纸片ABCD的顶点B与原点O重合,BC边放在x轴的正半轴上,AB=3,AD=6,将纸片沿过点M的直线...
- 如图, 已知直线分别与轴,轴交于两点, 点在轴上. 以点为圆心的⊙与直线相切于点, 连接.(1) 求证:∽;(2)如果⊙的半径为, 求出点...
- 抛物线y=(x-1)2-2的顶点坐标是A.(-1,2)B.(1,-2)C.(1,2)D.(-1,-2)
- 某商人开始时,将进价为每件8元的某种商品按每件10元出售,每天可售出100件.他想采用提高售价的办法来增加利润,经试验,发...