本试题 “关于x的不等式a-xx+b<0(a+b)>0的解集是( )A.{x|x>a}B.{x|x<-b,或x>a}C.{x|x<a,或x>-b}D.{x|-b<x<a}” 主要考查您对一元二次不等式及其解法
一元高次(二次以上)不等式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 一元二次不等式及其解法
- 一元高次(二次以上)不等式
一元二次不等式的概念:
只含有一个未知数,并且未知数的最高次数是2 的不等式称为一元二次不等式.
一元二次不等式的解集:
使某个一元二次不等式成立的x的值叫做这个一元二次不等式的解,一元二次不等式的所有解组成的集合叫做这个一元二次不等式的解集。
同解不等式:
如果两个不等式的解集相同,那么这两个不等式叫做同解不等式,如果一个不等式变形为另一个不等式时,这两个不等式是同解不等式,那么这种变形叫做不等式的同解变形。
二次函数的图象、一元二次方程的根、一元二次不等式的解集间的关系:
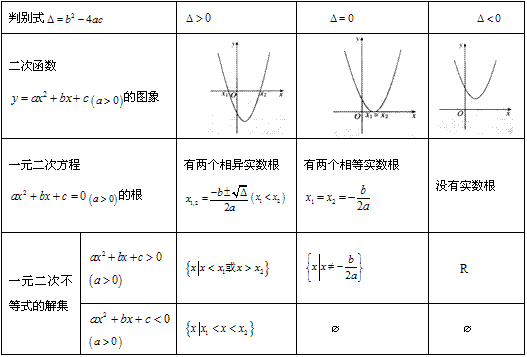
解不等式的过程:
解不等式的过程就是将不等式进行同解变形,化为最简形式的同解不等式的过程.变形时要注意条件的限制,比如:分母是否有意义,定义域是否有限制等.
解一元二次不等式的一般步骤为:
(1)对不等式变形,使一端为零且二次项系数大于零;(2)计算相应的判别式;(3)当△≥0时,求出相应的一元二次方程的根;(4)根据二次函数图象写出一元二次不等式的解集.
解含有参数的一元二次不等式:
(1)要以二次项系数与零的大小作为分类标准进行分类讨论;(2)转化为标准形式的一元二次不等式(即二次项系数大于零)后,再以判别式与零的大小作为分类标准进行分类讨论;(3)如果判别式大于零,但两根的大小还不能确定,此时再以两根的大小作为分类标准进行分类讨论。
元高次不等式的概念:
含有一个未知数且未知数的最高次数不小于3的不等式叫做一元高次不等式
一元高次不等式的解法:
①解一元高次不等式时,通常需进行因式分解,化为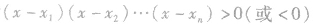 的形式,然后应用区间法化为不等式组或用数轴标根法求解集.
的形式,然后应用区间法化为不等式组或用数轴标根法求解集.
②用数轴标根法求解一元高次不等式的步骤如下:
a.化简:将原不等式化为和它同解的基本型不等式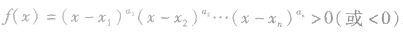 .其中
.其中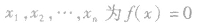 的n个根,它们两两不等,通常情况下,常以
的n个根,它们两两不等,通常情况下,常以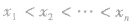 的形式出现,
的形式出现,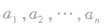 为相同因式的幂指数,它们均为自然数,可以相等;
为相同因式的幂指数,它们均为自然数,可以相等;
b.标根:将 标在数轴上,将数轴分成(n+1)个区间;
标在数轴上,将数轴分成(n+1)个区间;
c.求解:若 ,则从最右边区间的右上方开始画一条连续的曲线,依次穿过每一个零点(
,则从最右边区间的右上方开始画一条连续的曲线,依次穿过每一个零点(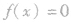 的根对应的数轴上的点),穿过最左边的零点后,曲线不再改变方向,向左下或左上的方向无限伸展.这样,不等式
的根对应的数轴上的点),穿过最左边的零点后,曲线不再改变方向,向左下或左上的方向无限伸展.这样,不等式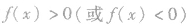 的解集就直观、清楚地表示在图上,这种方法叫穿针引线法(或数轴标根法);当
的解集就直观、清楚地表示在图上,这种方法叫穿针引线法(或数轴标根法);当 不全为l,即f(x)分解因式出现多重因式(即方程f(x)=0出现重根)时,对于奇次重因式对应的根,仍穿轴而过;对于偶次重因式对应的根,则应使曲线与轴相切.简言之,函数f(x)中有重因式时,曲线与轴的关系是"奇穿偶切".
不全为l,即f(x)分解因式出现多重因式(即方程f(x)=0出现重根)时,对于奇次重因式对应的根,仍穿轴而过;对于偶次重因式对应的根,则应使曲线与轴相切.简言之,函数f(x)中有重因式时,曲线与轴的关系是"奇穿偶切".
与“关于x的不等式a-xx+b<0(a+b)>0的解集是( )A.{x|x>a}B...”考查相似的试题有:
- 不等式ax2+bx+c>0的解集为{x|-1<x<2},则a(x2+1)+b(x-1)+c>2ax的解集为[ ]A、{x|0<x<3}B、{x|x<0或x>3}C、{x|-2...
- 不等式的解集是
- 不等式|2x-3|0的解集相同,则b+c=( )A.5B.6C.7D.8
- 若不等式(a2-3a+2) x2+(a-1)x+2>0恒成立,则a的取值范围______.
- 解关于x的不等式(x-1)(x-1a)<0,其中a≠0.
- 已知函数f(x)=3x2-6x-5.(1)求不等式f(x)>4的解集;(2)设g(x)=f(x)-2x2+mx,其中m∈R,求g(x)在区间[l,3]上的...
- 如果关于x的不等式x2+(a-1)x+1<0的解集为,则实数a的取值范围是( )。
- 当a≥0时解关于x的不等式 ax2-(a+2)x+2<0.
- 解下列不等式:(本小题满分12分若不等式对一切恒成立,试确定实数的取值范围.
- 已知a>0,b>0,不等式-b<1x<a的解集是______.