本试题 “判断。(对的打“√”.错的打“×”)(1)圆有无数条对称轴。[ ](2)正方形的面积和它的边长成正比例。[ ](3)甲队人数的等于乙队人数的,甲队与乙队的人数比是...” 主要考查您对轴对称,轴对称图形
分数的四则混合运算及应用
圆的周长
圆的面积
百分数的计算,百分数的应用题
正比例的意义,反比例的意义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 轴对称,轴对称图形
- 分数的四则混合运算及应用
- 圆的周长
- 圆的面积
- 百分数的计算,百分数的应用题
- 正比例的意义,反比例的意义
学过的图形中,线段、角、等腰三角形、等边三角形、长方形、正方形、等腰梯形、圆形、扇形都是轴对称图形,各自有不同数目的对称轴。
运算顺序:
分数四则混合运算的运算顺序和整数则混合运算的运算顺序相同:
一个算式里,如果只含有两级运算,先算第一级运算,再算第二级运算。
在含有括号的算式里,先算小括号里面的,再算中括号里面的,最后算括号外面的。
计算法则:
分数乘法的意义:
分数乘以整数 —×12 表示12个—是多少。
整数乘以真分数 12×— 表示12的—是多少。
分数乘以真分数 —×— —的—是多少。
一个数乘以带分数 —×1— 表示—的1—倍是多少。
分数加、减法的计算法则:
同分母分数相加减,分母不变,分子相加减。
异分母分数相加减,先通分,再按同分母方法计算。
分数乘除法计算方法:
分数乘法,分子相乘作分子,分母相乘作分母。
分数除法,乘以除数的倒数。
分数四则运算的意义:
加法:
把两个数合并成一个数的运算 把两个小数合并成一个小数的运算 把两个分数合并成一个分数的运算;
减法:
已知两个加数的和与其中一个加数,求另一个加数的运算 已知两个加数的和与其中一个加数,求另一个加数的运算 已知两个加数的和与其中一个加数,求另一个加数的运算;
乘法:
求几个相同加数的和的简便运算,小数乘整数的意义与整数乘法意义相同;
一个数乘纯小数就是求这个数的十分之几,百分之几……
除法:
已知两个因数的积与其中一个因数,求另一个因数的运算,与整数除法的意义相同.
圆的周长=直径×圆周率=2×半径×圆周率;C=πd=2πr。(r—半径,d—直径,π—圆周率)
圆的面积=半径×半径×圆周率;
S=π
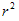 (r—半径,d—直径,π—圆周率)
(r—半径,d—直径,π—圆周率)圆环面积:
外圆面积-内圆面积;
S=π
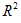 -π
-π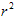 =π(
=π(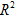 -
-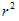 )(R—外圆半径,r—内圆半径)
)(R—外圆半径,r—内圆半径)
百分数应用题关系式:
利息的计算公式:利息=本金×利率×时间。
百分率:例:发芽率=发芽种子数÷试验种子数×100%
利率=利息÷本金×100%
折数=现价÷原价
成数=实际收成÷计划收成
税率=应纳税额÷总收入×100%
利润=售出价-成本,利润率=利润÷成本×100%=(售出价÷成本-1)×100%
折扣=实际售价÷原售价×100%(折扣<1)
浓度问题:
溶质的重量+溶剂的重量=溶液的重量;
溶质的重量÷溶液的重量×100%=浓度;
溶液的重量×浓度=溶质的重量;
溶质的重量÷浓度=溶液的重量。
正比例:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系,正比例的图像是一条直线;
用字母表示为如果用字母x和y表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用以下关系式表示: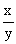 =k(一定);
=k(一定);
正比例关系两种相关联的量的变化规律:同时扩大,同时缩小,比值不变.正比例和反比例
反比例:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系;
如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定)。
反比例的意义:
成反比例的量包括三个数量,一个定量和两个变量。研究两个变量之间的扩大(或缩小)的变化关系。一种量发生变化,引起另一种量发生相反的变化。这两种量是反比例的量,它们的关系成反比例关系。
成反比例的量:
前提:两种相关的量(乘法关系)
要求:一个量变化,另一个量也随着变化,并且,这两个量中相对应的两个数的乘积一定。
结论:这两个量就叫做反比例的量,它们的关系叫做反比例关系。
正比例和反比例关系:
相同点:
①正比例和反比例都含有三个数量,在这三个数量中,均有一个定量、两个变量。
②在正、反比例的两个变量中,均是一个量变化,另一个量也随之变化。并且变化方式均属于扩大(乘以一个数)或缩小(除以一个数)若干倍的变化。
不同点:
①正比例的定量是两个变量中相对应的两个数的比值。反比例的定量是两个变量中相对应的两个数的积。
②正比例的图像时上升直线;反比例是曲线。
③公式不同:正比例是(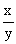 =k(一定)),反比例是(xy=k(一定))。
=k(一定)),反比例是(xy=k(一定))。
④规律不同:正比例是一个数缩小,另一个数也缩小,一个数扩大,另一个数也扩大;反比例是一个数缩小,另一个数就扩大,一个数扩大另一个数就缩小。
判断两种量成正比例、反比例或不成比例的方法:
(1)找出两种相关联的量。
(2)根据两种相关联的量之间的关系列出数量关系式。
(3)如果两种量中相对应的两个数的比值(也就是商)一定,就是成正比例的量;若积一定,就是反比例的量。
与“判断。(对的打“√”.错的打“×”)(1)圆有无数条对称轴。[ ]...”考查相似的试题有:
- 在正方形、等边三角形、扇形、圆中,对称轴最多的是( )A.等边三角形B.扇形C.圆D.正方形
- 文具店有72个新书包,第一天卖了13,第二天卖的书包数与第一天的比为1:2,第二天卖出书包多少个?
- B1一瓶纯牛奶,亮亮第一次喝了13,然后在瓶里兑满水,又接着喝去13.亮亮第一次喝的纯奶多.______.E1
- 在周长是8分米的正方形内剪掉一个最大的圆,圆的周长是______分米.
- 求如图中阴影部分面积:
- 甲是8,乙是5,则×100%= 60%表示[ ]A.乙比甲少60%B.甲比乙多60%C.甲是乙的60%D.乙是甲的60%
- 某农具厂计划生产农具2400件,实际制造3000件.超额完成计划的百分之几?
- (p099•许昌)买一辆汽车,分期付款要多加价7%,如果用现金购买只需按原价的98%付款,韦老师算了算,发现分期付款比现金购买...
- a年级有学生l9人,比女生多16%,女生有______人.
- 一根铁丝剪成同样长的段数与每段的长度.______.