本试题 “如图,已知点A的坐标为(1,0),点B在直线上运动,当线段AB最短时,点B的坐标为( )A.(0,0).B..C.D..” 主要考查您对有序数对
用坐标表示位置
用坐标表示平移
平面直角坐标系
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 有序数对
- 用坐标表示位置
- 用坐标表示平移
- 平面直角坐标系
通过像“九排七号” 、“第一排第五列”这样含有两个数的词来表示一个确定的位置,其中两个数各自表示不同的含义,例如前边的表示“排数”,后边的表示“号数”。我们把这种有顺序的两个数A与B组成的数对叫做有序数对,记做(A,B),常用在平面直角坐标系中。
平面上的点的坐标:
比如 (1,2) 就代表横坐标为 1 纵坐标为 2;而 (2,1) 就代表横坐标为 2 纵坐标为 1;
因为它们反过来表示的点不同所以是有序的。
利用有序数对,可以准确的表达出一个位置。
点的坐标用(a,b)表示,其顺序是横坐标在前,纵坐标在后,中间有“,”分开,横、纵坐标的位置不能颠倒。
平面内点的坐标是有序实数对,当a≠b时,(a,b)和(b,a)是两个不同点的坐标。
各象限内点的坐标的特征 :
点P(x,y)在第一象限
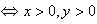 ;点P(x,y)在第二象限
;点P(x,y)在第二象限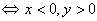
点P(x,y)在第三象限
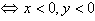 ;点P(x,y)在第四象限
;点P(x,y)在第四象限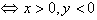
坐标轴上的点的特征:
点P(x,y)在x轴上
 y=0,x为任意实数
y=0,x为任意实数 点P(x,y)在y轴上
 x=0,y为任意实数
x=0,y为任意实数 点P(x,y)既在x轴上,又在y轴上
 x,y同时为零,即点P坐标为(0,0)。
x,y同时为零,即点P坐标为(0,0)。 点P(x,y)到坐标轴及原点的距离:
(1)点P(x,y)到x轴的距离等于|y|;
(2)点P(x,y)到y轴的距离等于|x|;
(3)点P(x,y)到原点的距离等于
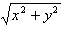 。
。 坐标表示位置步骤:
利用平面直角坐标系绘制区域内一些地点分布情况的平面图的过程如下:
(1)建立坐标系,选择一个适当的参照点为原点,确定X轴、y轴的正方向;
(2)根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;
(3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称。
把一个图形整体沿某一方向移动一定的距离, 图形的这种移动,叫做平移。
平移后图形的位置改变,形状、大小不变。
在平面直角坐标系内:
如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;
如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度。
图形平移与点的坐标变化之间的关系:
(1)左右平移:
原图形上的点(x、y),向右平移a个单位(x+a,y);
原图形上的点(x、y),向左平移a个单位(x-a,y);
(2)上、下平移:
原图形上的点(x、y),向上平移a个单位(x,y+b);
原图形上的点(x、y),向下平移a个单位(x,y-b)。
在平面内画两条互相垂直且有公共原点的数轴,就组成了平面直角坐标系。
其中,水平的数轴叫做x轴或横轴,取向右为正方向;
铅直的数轴叫做y轴或纵轴,取向上为正方向;
两轴的交点O(即公共的原点)叫做直角坐标系的原点;
建立了直角坐标系的平面,叫做坐标平面。
为了便于描述坐标平面内点的位置,把坐标平面被x轴和y轴分割而成的四个部分,分别叫做第一象限、第二象限、第三象限、第四象限。
注意:x轴和y轴上的点,不属于任何象限。
特殊位置的点的坐标的特点:
1.x轴上的点的纵坐标为零;y轴上的点的横坐标为零。
2.第一、三象限角平分线上的点横、纵坐标相等;第二、四象限角平分线上的点横、纵坐标互为相反数。
3.在任意的两点中,如果两点的横坐标相同,则两点的连线平行于纵轴;如果两点的纵坐标相同,则两点的连线平行于横轴。
4.点到轴及原点的距离
点到x轴的距离为|y|; 点到y轴的距离为|x|;点到原点的距离为x的平方加y的平方的平方根;
对称点:
1.关于x轴成轴对称的点的坐标,横坐标相同,纵坐标互为相反数。(横同纵反)
2.关于y轴成轴对称的点的坐标,纵坐标相同,横坐标互为相反数。(横反纵同)
3.关于原点成中心对称的点的坐标,横坐标与横坐标互为相反数,纵坐标与纵坐标互为相反数。(横纵皆反)
点的符号:
横坐标 纵坐标
第一象限:(+,+)正正
第二象限:(-,+)负正
第三象限:(-,-)负负
第四象限:(+,-)正负
x轴正半轴:(+,0)
x轴负半轴:(-,0)
y轴正半轴:(0,+)
y轴负半轴: (0,-)
x轴上的点的纵坐标为0,y轴上的点的横坐标为0。
原点:(0,0)
注:以数对形式(x,y)表示的坐标系中的点(如2,-4),“2”是x轴坐标,“-4”是y轴坐标。
其他公式:
1.坐标平面内的点与有序实数对一一对应。
2. 一三象限角平分线上的点横纵坐标相等。
3.二四象限角平分线上的点横纵坐标互为相反数。
4.一点上下平移,横坐标不变,即平行于y轴的直线上的点横坐标相同。
5.y轴上的点,横坐标都为0。
6.x轴上的点,纵坐标都为0。
7.坐标轴上的点不属于任何象限。
8.一个关于x轴对称的点横坐标不变,纵坐标变为原坐标的相反数。反之同样成立。
9.一个关于原点对称的点横纵坐标均为原坐标相反数。
10.与x轴做轴对称变换时,x不变,y变
11.与y轴做轴对称变换时,y不变,x变
12.与原点做轴对称变换时,y与x都变
应用:
用直角坐标原理在投影面上确定地面点平面位置的坐标系:
与数学上的直角坐标系不同的是,它的横轴为X轴,纵轴为Y轴。在投影面上,由投影带中央经线的投影为调轴、赤道投影为横轴(Y轴)以及它们的交点为原点的直角坐标系称为国家坐标系,否则称为独立坐标系。
坐标方法的简单应用:
1.用坐标表示地理位置
2.用坐标表示平移
在测量学中使用的平面直角坐标系统,包括高斯平面直角坐标系和独立平面直角坐标系。
通常选择:
高斯投影平面(在高斯投影时)或测区内平均水准面的切平面(在独立地区测量时)作为坐标平面;
纵坐标轴为x轴,向上(向北)为正;
横坐标轴为y轴,向右(向东)为正;
角度(方位角)从x轴正向开始按顺时针方向量取,象限也按逆时针方向编号。
与“如图,已知点A的坐标为(1,0),点B在直线上运动,当线段AB最...”考查相似的试题有:
- 将正整数按如图所示的规律在平面直角坐标系中进行排列,每个正整数对应一个整点坐标(x,y),且x,y均为整数。如数5对应的坐...
- 若点P(2m-1,-3)在第四象限,则m 的取值范围是( )A、m> B、m< C、m≥- D、m≤
- 在平面直角坐标系中,点P(-8,2012)在第( )象限.A.一B.二C.三D.四
- 在电影院内,若将“12排5座”简单记做(12,5),则“8排17座”可以表示为_______。
- 已知点A(-2,3),则点A关于x轴的对称点A1的坐标为( );关于y轴的对称点A2的坐标为( );关于原点的对称点A3的坐标为( )。
- 在平面直角坐标系中,已知线段AB的两个端点分别是A(-4,-1),B(l,1),将线段AB平移后得到线段A'B',若A'的坐标为(-2,2),则...
- 在平面直角坐标系中,点(-2, 3)在A.第一象限B.第二象限C.第三象限D.第四象限
- 下列各图中,是轴对称图形的是( )
- 已知:正方形中,,绕点顺时针旋转,它的两边分别交(或它们的延长线)于点.当绕点旋转到时(如图1),易证.(1)当绕点旋...
- 已知△ABC三个顶点的坐标分别是 A(– 3,–1)、B(1,3)、C(2,-3)小题1:在平面直角坐标系中描出各点并画出△ABC;小题2:求...