本试题 “(1)用红、黄、蓝、白四种不同颜色的鲜花布置如图一所示的花圃,要求同一区域上用同一种颜色鲜花,相邻区域用不同颜色鲜花,问共有多少种不同的摆放方案?(...” 主要考查您对随机事件及其概率
分步乘法计数原理
离散型随机变量及其分布列
离散型随机变量的期望与方差
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 随机事件及其概率
- 分步乘法计数原理
- 离散型随机变量及其分布列
- 离散型随机变量的期望与方差
随机事件的定义:
在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件叫做随机事件,随机事件通常用大写英文字母A、B、C等表示。
必然事件的定义:
必然会发生的事件叫做必然事件;
不可能事件:
肯定不会发生的事件叫做不可能事件;
概率的定义:
在大量进行重复试验时,事件A发生的频率 总是接近于某个常数,在它附近摆动。这时就把这个常数叫做事件A的概率,记作P(A)。
总是接近于某个常数,在它附近摆动。这时就把这个常数叫做事件A的概率,记作P(A)。
m,n的意义:事件A在n次试验中发生了m次。
因0≤m≤n,所以,0≤P(A)≤1,必然事件的概率为1,不可能发生的事件的概率0。
随机事件概率的定义:
对于给定的随机事件A,随着试验次数的增加,事件A发生的频率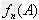 总是接近于区间[0,1]中的某个常数,我们就把这个常数叫做事件A的概率,记作P(A)。
总是接近于区间[0,1]中的某个常数,我们就把这个常数叫做事件A的概率,记作P(A)。
频率的稳定性:
即大量重复试验时,任何结果(事件)出现的频率尽管是随机的,却“稳定”在某一个常数附近,试验的次数越多,频率与这个常数的偏差大的可能性越小,这一常数就成为该事件的概率;
“频率”和“概率”这两个概念的区别是:
频率具有随机性,它反映的是某一随机事件出现的频繁程度,它反映的是随机事件出现的可能性;概率是一个客观常数,它反映了随机事件的属性。
分步原理:
完成一件事,需要n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,…做第n步有mn种不同的方法,那么完成这件事共有N=m1m2…mn不同的方法。
注:一步得出的结果都不是最后的结果,任何一步都不能独立地完成这件事,只有各个步骤都完成了,才能完成这件事。各步是关联的。
两种典型现象:
Ⅰ.涂颜色
(1)平面图涂颜色:先涂接触区域最多的一块;
(2)立体图涂颜色:先涂具有同一顶点的几个平面,其他平面每步涂法分类列举。
Ⅱ.映射
按步骤用A集合的每一个元素到B集合里选一个元素,可以重复选。
分类加法计数原理与分步乘法计数原理的关系:
(1)分类加法计数原理和分步乘法计数原理,解决的都是有关做一件事的不同方法的种数问题,都是计数的方法问题,二者的区别在于:分类加法计数原理针对的是分类问题,其各种方法之间是相互独立的,其中的任何一种方法都可以单独完成这件事;而分步乘法计数原理针对的是分步问题,各个步骤之间相互依存,只有各个步骤都完成,才算完成这件事,单独的一步或几步不能完成这件事.(2)两个计数原理的区别在于分类加法计数原理每次得到的都是最后结果,而分步乘法计数原理每步得到的都是中间结果,可以用下表表示: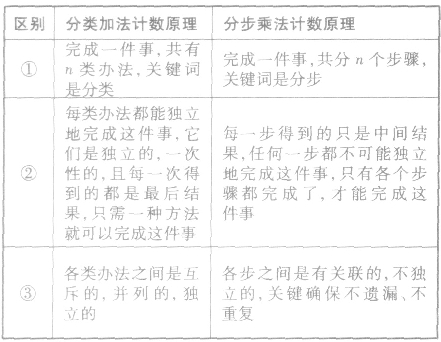
计数原理的选择:
如果完成一件事有n类办法,这n类办法彼此之间是相互独立的,无论哪一类办法中的哪一种方法都能完成这件事情,求完成这件事情的方法种数,就用分类加法计数原理;如果完成一件事情要分成n个步骤,各个步骤都是不可或缺的,需要依次完成所有的步骤,才能完成这件事情,而完成每一个步骤各有若干种不同的方法,求完成这件事情的方法种数,就用分步乘法计数原理,从思想方法的角度看,分类加法汁数原理是将问题进行,分步乘法计数原理是将问题进行,这两种思想方法贯穿解决本章应用问题的始终.
分步乘法计数原理的特点:
分步乘法计数原理的特点是在所有的各步之中,每一步中都要使用一种方法才能完成要做的事情,可利用图形
 来表示分步乘法计数原理,图中的去
来表示分步乘法计数原理,图中的去 强调要依次完成各个步骤才能完成要做的事情,从而共有
强调要依次完成各个步骤才能完成要做的事情,从而共有 种不同的方法可以完成这件事.
种不同的方法可以完成这件事.
分步的原则:
应用分步乘法计数原理解题时要注意以下几点:
①明确题目中所指的“完成一件事”是指什么事,单独用题目中所给的某种方法是不是能完成这件事,也就是说,是否必须经过几步才能完成这件事;
②完成这件事需要分成若干个步骤,只有每个步骤都完成了,才算完成这件事,缺少任何一步,这件事就不可能完成;
③根据题意,正确分步,要求各步之间必须连续,只有按照这n个步骤逐步地去做,才能完成这件事,各个步骤之中既不能重复也不能有遗漏.
分类加法计数原理的应用:
根据已知条件确定好分类标准后,分类应满足:完成一件事的任何一种方法,必属于某一类而且仅属于某一类,即,是确定的,可相加的.在解题时,应首先分清楚怎样才算完成这件事,完成这件事有n类途径、手段、方法等,其中的每一种都可以独立完成这件事.
分步乘法计数原理的应用:
应用分步乘法计数原理时,关键是确定分步的步骤,必须是连续做完几步,要不漏不重步,还要保证每个步骤之间是无关的.
两个原理的综合应用:
两个计数原理解决计数问题时,最重要的是在开始计算之前要进行仔细分析-----需要分类还是需要分步。
分类要做到“不重不漏”,分类后再分别对每一类进行计数,最后用分类加法计数原理求和,得到总数。
分步要做到“分步完整”,完成了所有步骤,恰好完成任务,当然步与步之间要相互独立.分步后再计算每一步的方法数,最后根据分步乘法计数原理,把完成每一步的方法数相乘,得到总数.
随机变量:
随着试验结果变化而变化的变量,常用字母ξ,η等来表示随机变量。
离散型随机变量:
所有取值可以一一列出的随机变量;
离散型随机变量的分布列:
如果离散型随机变量ξ可能取的值为x1,x2,x3,…,xn,…,而ξ取每一个值xi(i=1,2,3,…)的概率P(ξ=xi)=pi,以表格的形式表示如下:

上表称为离散型随机变量ξ的概率分布列,简称为ξ的分布列。
任一随机变量的分布列都具有下列性质:
(1)0≤pi≤1,(i=1,2,3,…);
(2)p1+p2+p3+…+pn+…=1;
(3)离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和。
求离散型随机变量分布列:
(1)先判断一个变量是否为离散型随机变量,主要看变量的值能否按一定的顺序一一列举出来.
(2)明确随机变量X可取哪些值.
(3)求x取每一个值的概率.(4)列成分布列表,
数学期望的定义:
称 为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
方差的定义:
称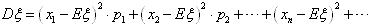 为ξ的均方差,简称为方差,
为ξ的均方差,简称为方差,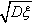 叫做随机变量ξ的标准差,记作:
叫做随机变量ξ的标准差,记作: 。
。
期望与方差的性质:
(1)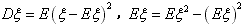 ;
;
(2)若η=aξ+b,则 ;
;
(3)若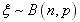 ,则
,则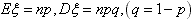 ;
;
(4)若ξ服从几何分布,则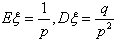 。
。
求均值(数学期望)的一般步骤:
(1)首先判断随机变量是否服从二点分布、二项分布或超几何分布,若服从,则直接用公式求均值.(2)若不服从特殊的分布,则先求出随机变量的分布列,再利用公式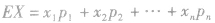 求均值。
求均值。
方差的求法:
(1)若随机变量X服从二点分布或二项分布,则直接利用方差公式可求.
(2)若随机变量X不服从特殊的分布时,求法为:
与“(1)用红、黄、蓝、白四种不同颜色的鲜花布置如图一所示的花...”考查相似的试题有:
- 已知集合A={0,3,6,9},从中任取两个元素分别作为点P(x,y)的横坐标与纵坐标,则点P恰好落入圆x2+y2=100内的概率是______.
- (本题满分13分)高三第一学期期末四校联考数学第I卷中共有8道选择题,每道选择题有4个选项,其中只有一个是正确的;评分标准...
- 袋中有大小相同的红球1只、黄球2只,从中任取1只,有放回地抽取3次.求:(1)3只全是红球的概率; (2)3只颜色全相同的概率...
- 乘积(a1+a2+…+a6)(b1+b2+…+b7)(c1+c2+…+c5)展开后,共有______项.
- 一个袋中有若干个大小相同的黑球、白球和红球.已知从袋中任意摸出1个球,得到黑球的概率是25;从袋中任意摸出2个球,至少得...
- (13分)某篮球队与其他6支篮球队依次进行6场比赛,每场均决出胜负,设这支篮球队与其他篮球队比赛中获胜的事件是独立的,并且...
- 若,则的值为( )A.B.C.D.
- 为了更好地服务于2010年世博会,上海某酒店随机地对最近入住的名旅客进行服务质量问卷调查,把旅客对住宿的舒适满意度与价格...
- 二十世纪50年代,日本熊本县水俣市的许多居民都患了运动失调、四肢麻木等症状,人们把它称为水俣病.经调查发现一家工厂排出...
- 某大厦的一部电梯从底层出发后只能在第6,7,8层停靠,若该电梯在底层有5个乘客,且每位乘客在这三层的每一层下电梯的概率为...