本试题 “某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品,现用两种新配方(分别称为A配方和B配方)做试验...” 主要考查您对用样本估计总体
离散型随机变量及其分布列
离散型随机变量的期望与方差
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 用样本估计总体
- 离散型随机变量及其分布列
- 离散型随机变量的期望与方差
样本估计总体的定义:
用样本的频率分布去估计总体的频率分布就是用样本估计总体。
用样本估计总体的特点:
用样本估计总体时,样本容量越大,样本对总体的估计也就越精确。相应地,搜集、整理、计算数据的工作量也就越大,随机抽样是经过数学证明了的可靠的方法,它对于估计总体特征是很有帮助的.
用样本估计总体方法总结:
用样本频率分布来估计总体分布的重点是频率分布表和频率分布直方图的绘制及用样本频率分布估计总体分布,在计数和计算时一定要准确,在绘制小矩形时,宽窄要一致,通过频率分布表和频率分布直方图可以对总体作出估计。
随机变量:
随着试验结果变化而变化的变量,常用字母ξ,η等来表示随机变量。
离散型随机变量:
所有取值可以一一列出的随机变量;
离散型随机变量的分布列:
如果离散型随机变量ξ可能取的值为x1,x2,x3,…,xn,…,而ξ取每一个值xi(i=1,2,3,…)的概率P(ξ=xi)=pi,以表格的形式表示如下:

上表称为离散型随机变量ξ的概率分布列,简称为ξ的分布列。
任一随机变量的分布列都具有下列性质:
(1)0≤pi≤1,(i=1,2,3,…);
(2)p1+p2+p3+…+pn+…=1;
(3)离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和。
求离散型随机变量分布列:
(1)先判断一个变量是否为离散型随机变量,主要看变量的值能否按一定的顺序一一列举出来.
(2)明确随机变量X可取哪些值.
(3)求x取每一个值的概率.(4)列成分布列表,
数学期望的定义:
称 为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
方差的定义:
称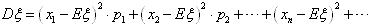 为ξ的均方差,简称为方差,
为ξ的均方差,简称为方差,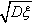 叫做随机变量ξ的标准差,记作:
叫做随机变量ξ的标准差,记作: 。
。
期望与方差的性质:
(1)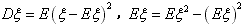 ;
;
(2)若η=aξ+b,则 ;
;
(3)若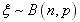 ,则
,则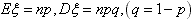 ;
;
(4)若ξ服从几何分布,则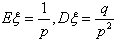 。
。
求均值(数学期望)的一般步骤:
(1)首先判断随机变量是否服从二点分布、二项分布或超几何分布,若服从,则直接用公式求均值.(2)若不服从特殊的分布,则先求出随机变量的分布列,再利用公式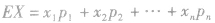 求均值。
求均值。
方差的求法:
(1)若随机变量X服从二点分布或二项分布,则直接利用方差公式可求.
(2)若随机变量X不服从特殊的分布时,求法为:
与“某种产品的质量以其质量指标值衡量,质量指标值越大表明质量...”考查相似的试题有:
- 为了解某种干电池的使用寿命,对其使用情况进行了追踪调查,统计情况如下表:寿命/h100~200200~300300~400400~500500~60...
- 在一家保险公司的董事会上,董事们就我国加入世界贸易组织(WTO)后公司的发展战略问题展开激烈讨论,其中一个议题是如何借鉴...
- 大学毕业的小张到甲、乙、丙三个单位应聘,各单位是否录用他相互独立,其被录用的概率分别为45、23、34(允许小张被多个单位...
- 某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生(I)分别求出按程序框图正确编程运...
- 件产品中,有件一等品,件二等品,件三等品,从这件产品中任取件求:(1)取出的件产品中一等品的件数的分布列和数学期望(2...
- 现有甲、乙两个靶,其射手向甲靶射击一次,命中的概率为34,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为23...
- 甲、乙两名教师进行乒乓球比赛,采用七局四胜制(先胜四局者获胜).若每一局比赛甲获胜的概率为23,乙获胜的概率为13.现已...
- 已知离散型随机变量X的分布列如表所示,若E(X)=0,D(X)=1,则a-b=( ) X -1 0 1 2 P a b c A. B. C.1 D.0
- 某班有名同学,一次考试后的数学成绩服从正态分布,则理论上分到分的人数是 ( ) A.32B.16C.8D.20
- 甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格...