本试题 “(本题13分)向量=(+1,),=(1,4cos(x+)),设函数=(∈R,且为常数).(1)若为任意实数,求的最小正周期;(2)若在[0,)上的最大值与最小值之和为7,求的值.” 主要考查您对向量数量积的含义及几何意义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 向量数量积的含义及几何意义
两个向量的夹角的定义:
对于非零向量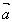 ,
,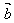 ,作
,作 称为向量
称为向量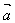 ,
,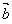 的夹角,当
的夹角,当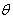 =0时,
=0时,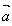 ,
,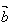 同向,当
同向,当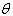 =π时,
=π时,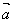 ,
,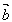 反向,
反向,
当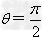 时,
时,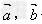 垂直。
垂直。
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
两个向量数量积的几何意义:
数量积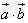 等于
等于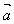 的模
的模 与
与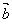 在
在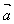 上的投影
上的投影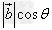 的乘积。
的乘积。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
发现相似题
与“(本题13分)向量=(+1,),=(1,4cos(x+)),设函数=(∈R,且...”考查相似的试题有:
- 单位向量与的夹角为,则( )A. B. C. D.
- 设 其中.(1)求的取值范围;(2)若,,求的值.
- 非零向量与满足且,则⊿ABC为( )A.三边均不等的三角形B.直角三角形C.等边三角形D.等腰非等边三角形
- 在中,是边上的一点,若,则=A.B.C.D.
- 如图,在中,,延长到,使,若,则 的值是 ( )A.B.C.D.
- 已知若和夹角为钝角,则的取值范围是( )A.B.C.D.
- 在▱ABCD中,=a,=b,=3,M为BC的中点,则=______(用a,b表示).
- 在边长为2的正三角形ABC中,为 A.B.C.D.
- 已知满足,且与之间有关系式,其中.(Ⅰ)用表示;(Ⅱ)求的最小值,并求此时与的夹角的大小.
- 设为同一平面内有相同起点的任意三个非零向量,且满足不共线,,,则的值一定等于( )A.以为两边的三角形的面积B.以为两边...