本试题 “B1(1)Χ-59Χ-49=23(2)65:6=Χ-15.E1” 主要考查您对解方程
解比例,比例的应用题
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 解方程
- 解比例,比例的应用题
解方程:
使方程左右两边相等的未知数的值叫做方程的解。
求方程的解的过程叫做解方程。
方程的解是一个值,解方程是求方程的解的演算过程。
检验方法:
求出未知数的值分别代入原方程的两边计算(即含有字母的式子的值),如果原方程等号左右两边相等,则所求得的未知数的值是原方程的解。
解方程依据:
方程依靠等式各部分的关系,和加减乘除各部分的关系:
加数+加数=和,和-其中一个加数=另一个加数,差+减数=被减数,
被减数-减数=差,被减数-差=减数,
因数×因数=积,积÷一个因数=另一个因数,
被除数÷除数=商,被除数÷商=除数,商×除数=被除数。
使方程左右两边相等的未知数的值叫做方程的解。
求方程的解的过程叫做解方程。
方程的解是一个值,解方程是求方程的解的演算过程。
检验方法:
求出未知数的值分别代入原方程的两边计算(即含有字母的式子的值),如果原方程等号左右两边相等,则所求得的未知数的值是原方程的解。
解方程依据:
方程依靠等式各部分的关系,和加减乘除各部分的关系:
加数+加数=和,和-其中一个加数=另一个加数,差+减数=被减数,
被减数-减数=差,被减数-差=减数,
因数×因数=积,积÷一个因数=另一个因数,
被除数÷除数=商,被除数÷商=除数,商×除数=被除数。
解比例:
求比例中的未知项,叫做解比例。
根据比例的基本性质(即交叉相乘),如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。求比例中的未知项,叫做解比例。解比例是利用比例的基本性质:在比例中,两个外项的积等于两个内项的积。再转化成方程。
比例应用题:
是小学六年级奥数中的一个重要内容。它既是整数应用题的继续与深化,又是学习更多数学知识的重要基础,同时,这类题又有着自身的特点和解题的规律。在处理几个量的倍比关系时,比例应用题与分数百分数应用题间有很多相似之处,但利用比例处理问题要方便灵活得多。
要解决好此类问题,须注意灵活运用画线段示意图等手段,多角度、多侧面思考问题。在解题过程中,要善于掌握对应、假设、转化等多种解题方法,在寻找正确的解题方法的同时,不断地开拓解题思路。
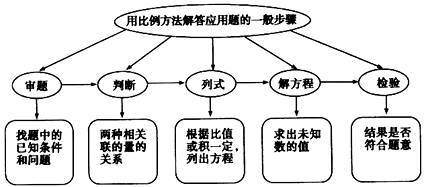
用比例方法解应用题的一般步骤:
发现相似题
与“B1(1)Χ-59Χ-49=23(2)65:6=Χ-15.E1”考查相似的试题有:
- 解下列方程.7(x-4.3)=25.2;(1.2x+3.5)×5=35.5.
- x=5是方程( )的解. A.4x-2=10 B.19-2x=7 C.2(x+3)=18 D.3.5x+1.7x=26
- 解方程.(1)40%X=120(2)X+4X=250(3)X-150=50%X.
- 方程2.5x +4.8=4.8,x的值是没有的,所以没有解。[ ]
- 解方程.x+0.8=1.7x-3.2=7.62.5+x=17.55x=24x÷0.6=4.20.7x=0.84.
- 如图,两个用皮带连在一起的皮带轮,大轮与小轮直径的比是3:1.那么,大轮转动100圈,小轮转动______圈.
- 填空.①一个分数的分子和分母的和是22,如果分子和分母分增加3后,化简后变成34,原来这个分数是______.②有一列数:1、4、7...
- 一张等腰三角形纸片,底和高的比是8:3.把它沿底边上的高剪开,可以拼成一个长方形.拼成的长方形的周长是28厘米,原来这张...
- 甲数的14和乙数13相等,则甲乙两数的比是 4:3______.
- (n0下0•萝岗区)一种消毒液包装纸4写明:清洗浴缸时需要将消毒液和清水按下﹕400配制.陈老师倒出这种消毒液下0克清洗浴缸,...