本试题 “下列正确的有[ ]A.角度大小与边的长短有关B.只要能被2除尽的数就是偶数C.0.80的计数单位是0.01D.圆的面积与半径的平方成正比例E.体积1dm3的长方体盒子放...” 主要考查您对小数的产生及意义
直线,射线,线段,角,度
长方体的体积
正比例的意义,反比例的意义
奇数,偶数
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 小数的产生及意义
- 直线,射线,线段,角,度
- 长方体的体积
- 正比例的意义,反比例的意义
- 奇数,偶数
在实际测量和计算时,往往不能正好得到整数的结果,这时常用小数来表示。由于日常生活和生产的需要,从而产生了小数。
小数位间的进率:
小数点右边第一位叫十分位,计数单位是十分之一(0.1),第二位叫百分位,计数单位是百分之一(0.01)……小数部分最大的计数单位是十分之一,没有最小的计数单位。
0.1
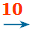 0.01
0.01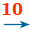 0.001…
0.001…小数的意义:
1、分母是10、100、1000…的分数,可以用小数表示。这就是小数的意义。
把1米看成一个整体,把一个整体平均分成10份、100份、1000份…这样的一份或几份可以用分母是10、100、1000…的分数来表示,也就可以用小数来表示。
我们可以理解:
一位小数:表示把一个整体平均分成10份,取了其中的一份或几份。
二位小数:表示把一个整体平均分成100份,取了其中的一份或几份。
三位小数:表示把一个整体平均分成1000份,取了其中的一份或几份。
如:0.36表示把整体“1”平均分成(100)份,取其中的(36)份。
直线:
把线段的两端无限延长,可以得到一条直线;
直线l,直线AB
射线:
把线段的一端无限延长,可以得到一条射线;
射线AB
射线有一个端点,直线没有端点。
线段:
用直尺把两点连接起来,就可以得到一条线段;线段是直线的一部分。
线段AB,线段a
线段有两个端点,它的长度是有限的,线段的长就是两点间的距离;
角:
从一点引出两条射线,就组成一个角。通常用符号“∠”来表示,角的大小看两条边叉开的大小,叉开的越大,角就越大。
角的大小与角两条边的长短没有关系。
角的计量单位:
角的计量单位是“度”,用符号“°”表示,把半圆分成180等份,每一份所对的角的大小是1度,记作1°。
直线的性质:两点确定一条直线,直线长度是无限的
线段的性质:两点之间线段最短.
射线的性质:射线的长度是无限的
各种图线的表示方法:
直线:一个小写字母或两个大写字母.但前面必须加“直线”两字,如:直线l;直线m,直线AB;直线CD.
射线:一个小写字母或端点的大写字母和射线上的一个大写字母,前面必须加 “射线”两字.如:射线a;射线OA.
线段:用表示端点的大写字母表示,如线段AB;用一个小写字母表示,如线段a.
长方体的体积=长×宽×高;V=abh。
长方体的体积=底面积×高;V=sh。
正比例:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系,正比例的图像是一条直线;
用字母表示为如果用字母x和y表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用以下关系式表示: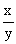 =k(一定);
=k(一定);
正比例关系两种相关联的量的变化规律:同时扩大,同时缩小,比值不变.正比例和反比例
反比例:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系;
如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定)。
反比例的意义:
成反比例的量包括三个数量,一个定量和两个变量。研究两个变量之间的扩大(或缩小)的变化关系。一种量发生变化,引起另一种量发生相反的变化。这两种量是反比例的量,它们的关系成反比例关系。
成反比例的量:
前提:两种相关的量(乘法关系)
要求:一个量变化,另一个量也随着变化,并且,这两个量中相对应的两个数的乘积一定。
结论:这两个量就叫做反比例的量,它们的关系叫做反比例关系。
正比例和反比例关系:
相同点:
①正比例和反比例都含有三个数量,在这三个数量中,均有一个定量、两个变量。
②在正、反比例的两个变量中,均是一个量变化,另一个量也随之变化。并且变化方式均属于扩大(乘以一个数)或缩小(除以一个数)若干倍的变化。
不同点:
①正比例的定量是两个变量中相对应的两个数的比值。反比例的定量是两个变量中相对应的两个数的积。
②正比例的图像时上升直线;反比例是曲线。
③公式不同:正比例是(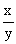 =k(一定)),反比例是(xy=k(一定))。
=k(一定)),反比例是(xy=k(一定))。
④规律不同:正比例是一个数缩小,另一个数也缩小,一个数扩大,另一个数也扩大;反比例是一个数缩小,另一个数就扩大,一个数扩大另一个数就缩小。
判断两种量成正比例、反比例或不成比例的方法:
(1)找出两种相关联的量。
(2)根据两种相关联的量之间的关系列出数量关系式。
(3)如果两种量中相对应的两个数的比值(也就是商)一定,就是成正比例的量;若积一定,就是反比例的量。
在自然数中,能被2整除的数,叫做偶数;不能被2整除的数是奇数。
奇数偶数性质:
偶数±偶数=偶数 奇数±奇数=偶数
偶数±奇数=奇数 奇数×奇数=奇数
偶数×偶数=偶数 奇数×偶数=偶数
0是一个特殊的偶数:
它既是正偶数与负偶数的分界线,又是正奇数与负奇数的分水岭。
与“下列正确的有[ ]A.角度大小与边的长短有关B.只要能被2除尽...”考查相似的试题有:
- 指针式钟表的表面上,1大格是( )度,1小格是( )度。( )点整或( )点整时时针和分针成直角。
- 取一个圆纸片,怎样才能找到圆心?对折几次才能得到180。、90。、45。的角?
- 一个角是50。,用放大2倍的放大镜来观察是[ ]A.50。B. 100。C.不能确定多少度
- 一个学习小组的四名同学观察并测量了一个长方体.刘星说:“如果高再增加2分米,它恰好是一个正方体.”王尘说:“长方体的前后...
- 有一个不规则的铁块,把铁块放入装满水的容器内,溢出的水装在长15厘米,宽10厘米的长方体水槽中,量得水面高10厘米,算一算...
- 如果a×b=15,那么a和b成______比例.
- 把一车沙子堆成圆锥体,沙堆的占地面积和高成反比例.______.
- B1全班人数一定,出勤人数和出勤率( )比例.E1B2 A.成正 B.成反 C.不成 E2
- 三个连续偶数的和是12,它们的积是多少?
- 在下列数中,既是质数又是偶数的数是[ ]A.1B.2C.3