本试题 “观察图中的甲、乙两图,回答下列问题。(1)请简述由图甲变成图乙的形成过程,以D点为旋转中心,图甲中的△A'DF绕点D顺时针旋转90°得到图乙;(2)在图乙中,...” 主要考查您对三角形的周长和面积
图形旋转
相似三角形的性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 三角形的周长和面积
- 图形旋转
- 相似三角形的性质
三角形的概念:
由不在同意直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
构成三角形的元素:
边:组成三角形的线段叫做三角形的边;
顶点:相邻两边的公共端点叫做三角形的顶点;
内角:相邻两边所组成的角叫做三角形的内角,简称三角形的角。
三角形有下面三个特性:
(1)三角形有三条线段;
(2)三条线段不在同一直线上;
(3)首尾顺次相接。
三角形的表示:
用符号“△,顶点是A、B、C的三角形记作“△ABC”,读作ABC”。
三角形的分类:
(1)三角形按边的关系分类如下:
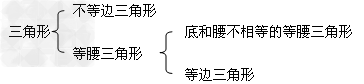 ;
;
(2)三角形按角的关系分类如下:

把边和角联系在一起,我们又有一种特殊的三角形:等腰直角三角形。它是两条直角边相等的直角三角形。
三角形的周长和面积:
三角形的周长等于三角形三边之和。
三角形面积=(底×高)÷2。
由不在同意直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
构成三角形的元素:
边:组成三角形的线段叫做三角形的边;
顶点:相邻两边的公共端点叫做三角形的顶点;
内角:相邻两边所组成的角叫做三角形的内角,简称三角形的角。
三角形有下面三个特性:
(1)三角形有三条线段;
(2)三条线段不在同一直线上;
(3)首尾顺次相接。
三角形的表示:
用符号“△,顶点是A、B、C的三角形记作“△ABC”,读作ABC”。
三角形的分类:
(1)三角形按边的关系分类如下:
 ;
;(2)三角形按角的关系分类如下:

把边和角联系在一起,我们又有一种特殊的三角形:等腰直角三角形。它是两条直角边相等的直角三角形。
三角形的周长和面积:
三角形的周长等于三角形三边之和。
三角形面积=(底×高)÷2。
定义:
在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。
图形的旋转是图形上的每一点在平面上绕着某个固定点旋转固定角度的位置移动,其中对应点到旋转中心的距离相等,对应线段的长度、对应角的大小相等,旋转前后图形的大小和形状没有改变。
图形旋转性质:
(1)对应点到旋转中心的距离相等。
(2)对应点与旋转中心所连线段的夹角等于旋转角。
旋转对称中心
把一个图形绕着一个点旋转一定的角度后,与原来的图形相吻合,这种图形叫做 旋转对称图形,这个定点叫做 旋转对称中心,旋转的角度叫做 旋转角。(旋转角大于0°小于360°)
在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。
图形的旋转是图形上的每一点在平面上绕着某个固定点旋转固定角度的位置移动,其中对应点到旋转中心的距离相等,对应线段的长度、对应角的大小相等,旋转前后图形的大小和形状没有改变。
图形旋转性质:
(1)对应点到旋转中心的距离相等。
(2)对应点与旋转中心所连线段的夹角等于旋转角。
旋转对称中心
把一个图形绕着一个点旋转一定的角度后,与原来的图形相吻合,这种图形叫做 旋转对称图形,这个定点叫做 旋转对称中心,旋转的角度叫做 旋转角。(旋转角大于0°小于360°)
相似三角形性质定理:
(1)相似三角形的对应角相等。
(2)相似三角形的对应边成比例。
(3)相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比。
(4)相似三角形的周长比等于相似比。
(5)相似三角形的面积比等于相似比的平方。
(6)相似三角形内切圆、外接圆直径比和周长比都和相似比相同,内切圆、外接圆面积比是相似比的平方
(7)若a/b =b/c,即b2=ac,b叫做a,c的比例中项
(8)c/d=a/b 等同于ad=bc.
(9)不必是在同一平面内的三角形里
①相似三角形对应角相等,对应边成比例.
②相似三角形对应高的比,对应中线的比和对应角平分线的比都等于相似比.
③相似三角形周长的比等于相似比
定理推论:
推论一:顶角或底角相等的两个等腰三角形相似。
推论二:腰和底对应成比例的两个等腰三角形相似。
推论三:有一个锐角相等的两个直角三角形相似。
推论四:直角三角形被斜边上的高分成的两个直角三角形和原三角形都相似。
推论五:如果一个三角形的两边和其中一边上的中线与另一个三角形的对应部分成比例,那么这两个三角形相似。
推论六:如果一个三角形的两边和第三边上的中线与另一个三角形的对应部分成比例,那么这两个三角形相似。
发现相似题
与“观察图中的甲、乙两图,回答下列问题。(1)请简述由图甲变成...”考查相似的试题有:
- 将图形按顺时针时针方向旋转270度后的图形是[ ]A.B.C.D.
- 如图,在等腰Rt△ABC中,∠CAB=90°,P是△ABC内一点,且PA=1,PB=3,PC=7.请利用旋转的方法求:∠CPA的大小.
- 如图是游乐园中的大型旋转车的简图,游人坐在旋转车的车斗中,任凭旋转车不停地旋转,但总是头朝上,绝不会掉下来.试问车斗...
- 如图,x轴、y轴上分别有两点A(3,0)、B(0,2),以点A为圆心,AB为半径的弧交x轴负半轴于点C,则点C的坐标为( )A.(-1...
- 下列两个三角形中,一定全等的是( )A.有一个角是40°,腰相等的两个等腰三角形;B.两个等边三角形;C.有一个角是100°,底...
- △ABC的面积为4cm2,D、E、F分别是AE,BC,CD的中点,则△BDF的面积为( )A、2 cm2, B、1 cm2, C、0.5 cm2, D、0.25 cm2,
- 已知:在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且BD⊥AE于D,CE⊥AE于E.(1)当直线AE处于如图①的位置时,有BD=DE+C...
- 如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=3。(1)在A...
- 已知△ABC∽△DEF,且△ABC的三边长分别为4,5,6,△DEF的一边长为2,则△DEF的周长为[ ]A.7.5B.6C.5或6D.5或6或7.5
- 如图,国旗上的五角星的五个角的度数是相同的,每一个角的度数都是 ( )A.B.C.D.