本试题 “在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是______.” 主要考查您对直线与圆的位置关系
圆与圆的位置关系
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 直线与圆的位置关系
- 圆与圆的位置关系
直线与圆的位置关系:
由直线与圆的公共点的个数,得出以下直线和圆的三种位置关系:
(1)相交:直线与圆有两个公共点时,叫做直线和圆相交,这时直线叫做圆的割线。
(2)相切:直线和圆有唯一公共点时,叫做直线和圆相切,这时直线叫做圆的切线,唯一的公共点叫做切点。
(3)相离:直线和圆没有公共点时,叫做直线和圆相离。
其图像如下: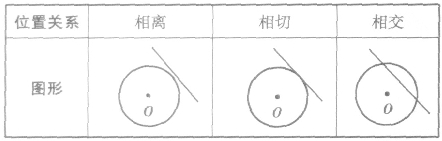
直线和圆的位置关系的性质:
(1)直线l和⊙O相交 d<r
d<r
(2)直线l和⊙O相切 d=r;
d=r;
(3)直线l和⊙O相离 d>r。
d>r。
直线与圆位置关系的判定方法:
(1)代数法:判断直线Ax+By+C=0和圆x2+y2+Dx+Ey+F=0的位置关系,可由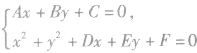
推出mx2+nx+p=0,利用判别式△进行判断.
△>0则直线与圆相交;
△=0则直线与圆相切;
△<0则直线与圆相离.
(2)几何法:已知直线Ax+By+C=0和圆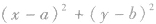
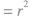 ,圆心到直线的距离
,圆心到直线的距离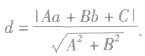
d<r则直线和圆相交;
d=r则直线和圆相切;
d>r则直线和圆相离.
特别提醒:
(1)上述两种方法,以利用圆心到直线的距离进行判定较为简捷,而判别式法也适用于直线与椭圆、双曲线、抛物线位置关系的判断.
(2)直线与圆相交,应抓住半径、弦心距、半弦长组成的直角三角形,可使解法简单.
直线与圆位置关系的判定方法列表如下:
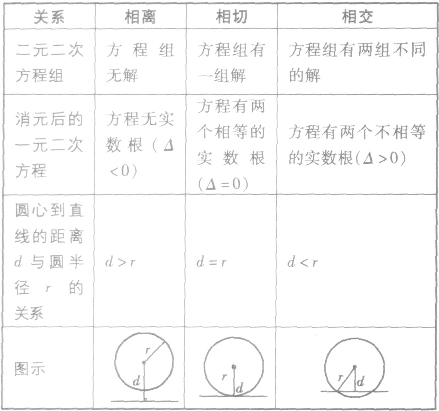
直线与圆相交的弦长公式:
(1)几何法:如图所示,直线l与圆C相交于A、B两点,线段AB的长即为l与圆相交的弦长。
设弦心距为d,半径为r,弦为AB,则有|AB|=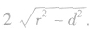
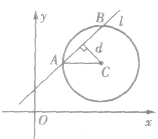
(2)代数法:直线l与圆交于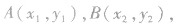 直线l的斜率为k,则有
直线l的斜率为k,则有
当直线AB的倾斜角为直角,即斜率不存在时,|AB|=
圆与圆的位置关系:
圆与圆有五种位置关系:相交、外离、外切、内切和内含。
圆与圆的位置关系的判断方法:
(1)利用圆心距和两圆半径比较大小(几何法)已知两圆
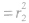 的圆心距为d
的圆心距为d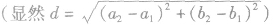 ,则位置关系表示如下:
,则位置关系表示如下: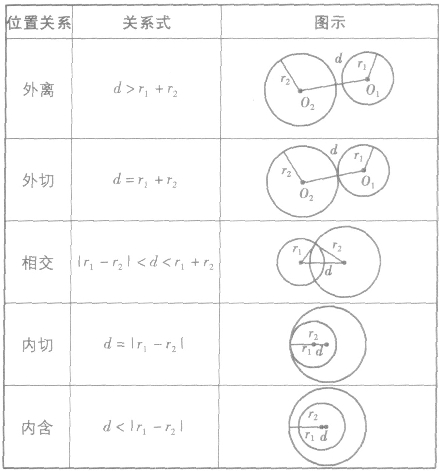
(2)利用两圆的交点进行判断(代数法)
设由两圆的方程组成的方程组为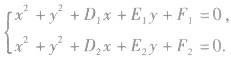
由此方程组得:有两组不同的实数解则两圆相交;有两组相同的实数解则两圆相切;无实数解则两圆相离.
两圆公切线条数的确定:
两圆的公切线的条数是由两圆的位置关系确定的,设两圆的圆心距为d,两圆的半径分别为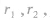
则当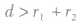 时,两圆外离,此时有四条公切线;
时,两圆外离,此时有四条公切线;
当 时,两圆外切,连心线过切点,此时有三条公切线,有外公切线两条,内公切线一条;
时,两圆外切,连心线过切点,此时有三条公切线,有外公切线两条,内公切线一条;
当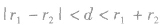 时,两圆相交,连心线垂直平分公共弦,有两条外公切线;
时,两圆相交,连心线垂直平分公共弦,有两条外公切线;
当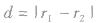 时,两圆内切,连心线过切点,此时只有一条公切线;
时,两圆内切,连心线过切点,此时只有一条公切线;
当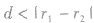 时,两圆内含,此时没有公切线。
时,两圆内含,此时没有公切线。
与“在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=...”考查相似的试题有:
- 已知Rt△ABC的两条直角边长分别为a、b,斜边长为c,则直线ax+by+c=0与圆x2+y2=1的位置关系是( ) A.相交 B.相切 C.相离 D...
- 已知:如图,圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为的椭圆,其左焦点为F,若P是圆O上一点,连接PF,过原...
- 已知半径为5的圆的圆心在x轴上,圆心的横坐标是整数,且与直线4x+3y-29=0相切.(1)求圆的方程;(2)若直线ax-y+5=0(a≠0)...
- 已知直线l:(2m+1)x+(m+1)y=7m+4,圆C:(x-1)2+(y-2)2=25.(1)判断直线l和圆C的位置关系;(2)若直线l和圆C相交,...
- 在圆x2+y2=5x内,过点(52,32)有n条弦的长度成等差数列,最短弦长为数列的首项a1,最长弦长为an,若n=10,那么公差d的值为___...
- 过原点且倾斜角为60 °的直线被圆x2+y2﹣4y=0所截得的弦长为( )
- 已知圆C的方程为x2+(y-4)2=4,点O是坐标原点.直线l:y=kx与圆C交于M,N两点.(Ⅰ)求k的取值范围;(Ⅱ)设Q(m,n)是线段...
- 设圆C与两圆(x+)2+y2=4,(x﹣)2+y2=4中的一个内切,另一个外切.(1)求C的圆心轨迹L的方程;(2)已知点M(,),F(,0...
- 设k为正实数,若满足条件x(x-k)≤y(k-y)的点(x,y)都被单位圆覆盖,则k的最大值为______.
- 已知圆C的圆心是直线x-y-1=0与x轴的交点,且圆C与直线3x-4y+2=0相切,则圆C的方程为______.