本试题 “本小题满分12分)已知抛物线(I)求p与m的值;(II)若斜率为—2的直线l与抛物线G交于P、Q两点,点M为抛物线G上一点,其横坐标为1,记直线PM的斜率为k1,直线Q...” 主要考查您对抛物线的定义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 抛物线的定义
抛物线的定义:
平面内与一个定点F和一条定直线l(F∈l)的距离相等的点的轨迹叫做抛物线,定点F叫做抛物线的焦点,定直线l叫做抛物线的准线,抛物线的定义也可以说成是:平面内与一个定点F和一条定直线l的距离的比等于1的点的轨迹.
抛物线中的有关概念:
| 定义 | 图形 | |
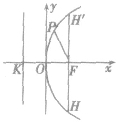
| 抛物线的弦、焦点弦 | 连结抛物线上任意两点的线段,叫做抛物线的弦. 过抛物线焦点的弦,叫做焦点弦 |
 |
| 抛物线的通径和焦参数 | 过焦点且垂直于抛物线的弦叫做抛物线的通径,通径长度的一半叫做抛物线的焦参数 | |
| 焦点半径 | 抛物线上一点P和焦点的连线,叫做点P的焦点半径或焦半径 | |
| 抛物线的焦准距 | 抛物线的焦点和它的准线间的距离,叫做焦准距,依据定义,显然有KO=OF, 即焦准距等于通径长的一半,焦准距用常数p表示 即焦准距等于通径长的一半,焦准距用常数p表示 |
抛物线的规律总结:
①在抛物线的定义中的定点F不在直线l上,否则动点的轨迹就是过点F且垂直于直线l的一条直线,而不再是抛物线;
②抛物线的定义中指明了抛物线上的点到焦点的距离与到准线的距离相等,故在一些问题中,二者可以互相转化,这是利用抛物线定义解题的关键.
发现相似题
与“本小题满分12分)已知抛物线(I)求p与m的值;(II)若斜率为...”考查相似的试题有:
- 抛物线 的焦点坐标为( ) .A.B.C.D.
- 已知⊙O:,为抛物线的焦点,为⊙O外一点,由作⊙O的切线与圆相切于点,且(1)求点P的轨迹C的方程(2)设A为抛物线准线上任意一...
- 抛物线的焦点坐标是____________________.
- 已知A、B是抛物线上的两点,O是抛物线的顶点,OA⊥OB.(I)求证:直线AB过定点M(4,0);(II)设弦AB的中点为P,求点P到直线...
- 抛物线上到直线的距离最近的点的坐标( )A.B.C.D.
- 某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划建成一个矩形的高科技工业园区.已知⊥,∥,且,,曲线段是以点...
- 若抛物线的顶点是双曲线的中心,焦点是双曲线的右顶点.(1)求抛物线的标准方程.(2)若直线过点交抛物线于两点,是否存在直线,...
- 抛物线的焦点坐标是___ ,
- 已知抛物线上的任意一点到该抛物线焦点的距离比该点到轴的距离多1.(1)求的值;(2)如图所示,过定点(2,0)且互相垂直的...
- 若抛物线y2=2px(p>0)上三点的横坐标成等差数列,那么这三点与焦点F的距离的关系是 ( )A.成等差数列B.成等比数列C.既成等...