本试题 “如图,∠1的正切值等于______.” 主要考查您对圆心角,圆周角,弧和弦
锐角三角函数的定义
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 圆心角,圆周角,弧和弦
- 锐角三角函数的定义
圆的定义:
在同一平面内,到定点的距离等于定长的点的集合叫做圆。这个定点叫做圆的圆心。图形一周的长度,就是圆的周长。
弧:
圆上任意两点间的部分叫做圆弧,简称弧。
弧用符号“⌒”表示以A,B为端点的弧记作“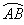 ”,读作“圆弧AB”或“弧AB”。
”,读作“圆弧AB”或“弧AB”。
优弧:大于半圆的弧(多用三个字母表示);
劣弧:小于半圆的弧(多用两个字母表示)
圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆。
弧、弦、弦心距、圆心角之间的关系定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等。
推论:在同圆或等圆中,如果两个圆的圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。
圆心角:
顶点在圆心的角叫做圆心角。
圆周角:
顶点在圆上,并且两边都和圆相交的角叫做圆周角。
圆周角的顶点在圆上,它的两边为圆的两条弦。
圆心角特征识别:
①顶点是圆心;
②两条边都与圆周相交。
计算公式:
①L(弧长)=n/180Xπr(n为圆心角度数,以下同);
②S(扇形面积) = n/360Xπr2;
③扇形圆心角n=(180L)/(πr)(度)。
④K=2Rsin(n/2) K=弦长;n=弦所对的圆心角,以度计。
圆心角定理:
圆心角的度数等于它所对的弧的度数。
理解:(定义)
(1)等弧对等圆心角
(2)把顶点在圆心的周角等分成360份时,每一份的圆心角是1°的角.
(3)因为在同圆中相等的圆心角所对的弧相等,所以整个圆也被等分成360份,这时,把每一份这样得到的弧叫做1°的弧.
(4)圆心角的度数和它们对的弧的度数相等.
推论:
在同圆或等圆中,如果(1)两个圆心角,(2)两条弧,(3)两条弦(4)两条弦上的弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等
与圆周角关系:
在同圆或等圆中,同弧或同弦所对的圆周角等于二分之一的圆心角。
定理证明:分三种情况讨论,始终做直径COD,利用等腰三角形等腰底角相等,外角等于两内角之和来证明。
圆周角定理推论:
圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角都等于这条弧所对的圆心角的一半。
①圆周角度数定理:圆周角的度数等于它所对的弧的度数的一半。
②同圆或等圆中,圆周角等于它所对的弧上的圆心角的一半。
③同圆或等圆中,同弧或等弧所对的圆周角相等,相等圆周角所对的弧也相等。(不在同圆或等圆中其实也相等的。注:仅限这一条。)
④半圆(或直径)所对圆周角是直角,90°的圆周角所对的弦是直径。
⑤圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
⑥在同圆或等圆中,圆周角相等<=>弧相等<=>弦相等。
锐角三角函数:
锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec),余割(csc)都叫做角A的锐角三角函数。
初中学习的 锐角三角函数值的定义方法是在直角三角形中定义的,所以在初中阶段求锐角的三角函数值,都是通过构造直角三角形来完成的,即把这个角放到某个直角三角形中。所谓锐角三角函数是指:我们初中研究的都是锐角的三角函数。初中研究的锐角的三角函数为:正弦(sin),余弦(cos),正切(tan)。
正弦:在直角三角形中,锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即 ;
;
余弦:在直角三角形中,锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即 ;
;
正切:在直角三角形中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即 ,
,
锐角A的正弦、余弦、正切都叫做A的锐角三角函数。
锐角三角函数的增减性:
1.锐角三角函数值都是正值
2.当角度在0°~90°间变化时,
正弦值随着角度的增大(或减小)而增大(或减小) ,余弦值随着角度的增大(或减小)而减小(或增大) ;
正切值随着角度的增大(或减小)而增大(或减小) ,余切值随着角度的增大(或减小)而减小(或增大);
正割值随着角度的增大(或减小)而增大(或减小),余割值随着角度的增大(或减小)而减小(或增大)。
3.当角度在0°≤A≤90°间变化时,0≤sinA≤1, 1≥cosA≥0;当角度在0°<A0, cotA>0。
锐角三角函数的关系式:
同角三角函数基本关系式
tanα·cotα=1
sin2α·cos2α=1
cos2α·sin2α=1
sinα/cosα=tanα=secα/cscα
cosα/sinα=cotα=cscα/secα
(sinα)2+(cosα)2=1
1+tanα=secα
1+cotα=cscα
诱导公式
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
cot(-α)=-cotα
sin(π/2-α)=cosα
cos(π/2-α)=sinα
tan(π/2-α)=cotα
cot(π/2-α)=tanα
sin(π/2+α)=cosα
cos(π/2+α)=-sinα
tan(π/2+α)=-cotα
cot(π/2+α)=-tanα
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
cot(π+α)=cotα
sin(3π/2-α)=-cosα
cos(3π/2-α)=-sinα
tan(3π/2-α)=cotα
cot(3π/2-α)=tanα
sin(3π/2+α)=-cosα
cos(3π/2+α)=sinα
tan(3π/2+α)=-cotα
cot(3π/2+α)=-tanα
sin(2π-α)=-sinα
cos(2π-α)=cosα
tan(2π-α)=-tanα
cot(2π-α)=-cotα
sin(2kπ+α)=sinα
cos(2kπ+α)=cosα
tan(2kπ+α)=tanα
cot(2kπ+α)=cotα(其中k∈Z)
二倍角、三倍角的正弦、余弦和正切公式
Sin(2α)=2sinαcosα
Cos(2α)=(cosα)2-(sinα)2=2(cosα)2-1=1-2(sinα)2
Tan(2α)=2tanα/(1-tanα)
sin(3α)=3sinα-4sin3α=4sinα·sin(60°+α)sin(60°-α)
cos(3α)=4cos3α-3cosα=4cosα·cos(60°+α)cos(60°-α)
tan(3α)=(3tanα-tan3α)/(1-3tan2α)=tanαtan(π/3+α)tan(π/3-α)
和差化积、积化和差公式
sinα+sinβ=2sin[(α+β)/2]·cos[(α-β)/2]
sinα-sinβ=2cos[(α+β)/2]·sin[(α-β)/2]
cosα+cosβ=2cos[(α+β)/2]·cos[(α-β)/2]
cosα-cosβ=-2sin[(α+β)/2]·sin[(α-β)/2]
sinαcosβ=-[sin(α+β)+sin(α-β)]
sinαsinβ=-[1][cos(α+β)-cos(α-β)]/2
cosαcosβ=[cos(α+β)+cos(α-β)]/2
sinαcosβ=[sin(α+β)+sin(α-β)]/2
cosαsinβ=[sin(α+β)-sin(α-β)]/2
与“如图,∠1的正切值等于______.”考查相似的试题有:
- 如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD=[ ]A.20°B.40°C.50°D.80°
- 如图所示,已知AE为⊙O的直径,AD为△ABC的BC边上的高.(1)求证:∠BAE=∠DAC;(2)若AB=10,AD=6,CD=23,求⊙O的面积.
- 如图,已知以O为圆心的两个同心圆中,大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于A、B,求证:AC=BD.
- 如图,△为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O 上,∠BAC=35°,则∠ADC=( )度.
- 如图,将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙的切点为A、B,点P是桌子边缘上一点,则∠APB等于A.30°B.45°C.60°D....
- △ABC内接于⊙O,已知∠A=70°,则∠BOC=______.
- 如图所示,某人站在楼顶观测对面的笔直的旗杆AB.已知观测点C到旗杆的距离(CE的长度)为8m,测得旗杆的仰角∠ECA为30°,旗杆底...
- 在Rt△ABC中,∠C=90°,则下面关系中不正确的是( )A.c=B.c=C.a=b·tanAD.b=a·cosB
- 在Rt△ABC中,∠C=90°,如果已知∠A的对边a和∠B,则c等于( )A.aSinBB.bCosBC.aSinBD.aCosB
- 如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E。(1)求证:△ACE∽△CBE;(2)若AB=8,设OE=x(0<x<4),CE2=y,请求出y关于x的函...