本试题 “如图,已知⊙O和⊙O′相交于A、B两点,过点A作⊙O′的切线交⊙O于点C,过点B作两圆的割线分别交⊙O、⊙O′于E、F,EF与AC相交于点P。 (1)求证:PA·PE=PC·PF;(2)求...” 主要考查您对勾股定理
相似三角形的性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 勾股定理
- 相似三角形的性质
勾股定理:
直角三角形两直角边(即“勾”,“股”)边长平方和等于斜边(即“弦”)边长的平方。也就是说,如果直角三角形的两直角边长分别为a,b,斜边长为c,那么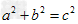 。
。
勾股定理只适用于直角三角形,应用于解决直角三角形中的线段求值问题。
定理作用
⑴勾股定理是联系数学中最基本也是最原始的两个对象——数与形的第一定理。
⑵勾股定理导致不可通约量的发现,从而深刻揭示了数与量的区别,即所谓“无理数"与有理数的差别,这就是所谓第一次数学危机。
⑶勾股定理开始把数学由计算与测量的技术转变为证明与推理的科学。
⑷勾股定理中的公式是第一个不定方程,也是最早得出完整解答的不定方程,它一方面引导到各式各样的不定方程,包括著名的费尔马大定理,另一方面也为不定方程的解题程序树立了一个范式。
勾股定理的应用:
数学
从勾股定理出发开平方、开立方、求圆周率等,运用勾股定理数学家还发现了无理数。
勾股定理在几何学中的实际应用非常广泛,较早的应用案例有《九章算术》中的一题:“今有池,芳一丈,薛生其中央,出水一尺,引薛赴岸,适与岸齐,问水深几何?答曰:"一十二尺"。
生活
勾股定理在生活中的应用也较广泛,举例说明如下:
1、挑选投影设备时需要选择最佳的投影屏幕尺寸。以教室为例,最佳的屏幕尺寸主要取决于使用空间的面积,从而计划好学生座位的多少和位置的安排。选购的关键则是选择适合学生的屏幕而不是选择适合投影机的屏幕,也就是说要把学生的视觉感受放在第一位。一般来说在选购时可参照三点:
第一,屏幕高度大约等于从屏幕到学生最后一排座位的距离的1/6;
第二,屏幕到第一排座位的距离应大于2倍屏幕的高度;
第三,屏幕底部应离观众席所在地面最少122厘米。
屏幕的尺寸是以其对角线的大小来定义的。一般视频图像的宽高比为4:3,教育幕为正方形。如一个72英寸的屏幕,根据勾股定理,很快就能得出屏幕的宽为1.5m,高为1.1m。
2、2005年珠峰高度复测行动。
测量珠峰的一种方法是传统的经典测量方法,就是把高程引到珠峰脚下,当精确高程传递至珠峰脚下的6个峰顶交会测量点时,通过在峰顶竖立的测量觇标,运用“勾股定理”的基本原理测定珠峰高程,配合水准测量、三角测量、导线测量等方式,获得的数据进行重力、大气等多方面改正计算,最终得到珠峰高程的有效数据。
通俗来说,就是分三步走:
第一步,先在珠峰脚下选定较容易的、能够架设水准仪器的测量点,先把这些点的精确高程确定下来;
第二步,在珠峰峰顶架起觇标,运用三角几何学中“勾股定理”的基本原理,推算出珠峰峰顶相对于这几个点的高程差;
第三步,获得的高程数据要进行重力、大气等多方面的改正计算,最终确定珠峰高程测量的有效数据。
直角三角形两直角边(即“勾”,“股”)边长平方和等于斜边(即“弦”)边长的平方。也就是说,如果直角三角形的两直角边长分别为a,b,斜边长为c,那么
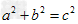 。
。勾股定理只适用于直角三角形,应用于解决直角三角形中的线段求值问题。
定理作用
⑴勾股定理是联系数学中最基本也是最原始的两个对象——数与形的第一定理。
⑵勾股定理导致不可通约量的发现,从而深刻揭示了数与量的区别,即所谓“无理数"与有理数的差别,这就是所谓第一次数学危机。
⑶勾股定理开始把数学由计算与测量的技术转变为证明与推理的科学。
⑷勾股定理中的公式是第一个不定方程,也是最早得出完整解答的不定方程,它一方面引导到各式各样的不定方程,包括著名的费尔马大定理,另一方面也为不定方程的解题程序树立了一个范式。
勾股定理的应用:
数学
从勾股定理出发开平方、开立方、求圆周率等,运用勾股定理数学家还发现了无理数。
勾股定理在几何学中的实际应用非常广泛,较早的应用案例有《九章算术》中的一题:“今有池,芳一丈,薛生其中央,出水一尺,引薛赴岸,适与岸齐,问水深几何?答曰:"一十二尺"。
生活
勾股定理在生活中的应用也较广泛,举例说明如下:
1、挑选投影设备时需要选择最佳的投影屏幕尺寸。以教室为例,最佳的屏幕尺寸主要取决于使用空间的面积,从而计划好学生座位的多少和位置的安排。选购的关键则是选择适合学生的屏幕而不是选择适合投影机的屏幕,也就是说要把学生的视觉感受放在第一位。一般来说在选购时可参照三点:
第一,屏幕高度大约等于从屏幕到学生最后一排座位的距离的1/6;
第二,屏幕到第一排座位的距离应大于2倍屏幕的高度;
第三,屏幕底部应离观众席所在地面最少122厘米。
屏幕的尺寸是以其对角线的大小来定义的。一般视频图像的宽高比为4:3,教育幕为正方形。如一个72英寸的屏幕,根据勾股定理,很快就能得出屏幕的宽为1.5m,高为1.1m。
2、2005年珠峰高度复测行动。
测量珠峰的一种方法是传统的经典测量方法,就是把高程引到珠峰脚下,当精确高程传递至珠峰脚下的6个峰顶交会测量点时,通过在峰顶竖立的测量觇标,运用“勾股定理”的基本原理测定珠峰高程,配合水准测量、三角测量、导线测量等方式,获得的数据进行重力、大气等多方面改正计算,最终得到珠峰高程的有效数据。
通俗来说,就是分三步走:
第一步,先在珠峰脚下选定较容易的、能够架设水准仪器的测量点,先把这些点的精确高程确定下来;
第二步,在珠峰峰顶架起觇标,运用三角几何学中“勾股定理”的基本原理,推算出珠峰峰顶相对于这几个点的高程差;
第三步,获得的高程数据要进行重力、大气等多方面的改正计算,最终确定珠峰高程测量的有效数据。
相似三角形性质定理:
(1)相似三角形的对应角相等。
(2)相似三角形的对应边成比例。
(3)相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比。
(4)相似三角形的周长比等于相似比。
(5)相似三角形的面积比等于相似比的平方。
(6)相似三角形内切圆、外接圆直径比和周长比都和相似比相同,内切圆、外接圆面积比是相似比的平方
(7)若a/b =b/c,即b2=ac,b叫做a,c的比例中项
(8)c/d=a/b 等同于ad=bc.
(9)不必是在同一平面内的三角形里
①相似三角形对应角相等,对应边成比例.
②相似三角形对应高的比,对应中线的比和对应角平分线的比都等于相似比.
③相似三角形周长的比等于相似比
定理推论:
推论一:顶角或底角相等的两个等腰三角形相似。
推论二:腰和底对应成比例的两个等腰三角形相似。
推论三:有一个锐角相等的两个直角三角形相似。
推论四:直角三角形被斜边上的高分成的两个直角三角形和原三角形都相似。
推论五:如果一个三角形的两边和其中一边上的中线与另一个三角形的对应部分成比例,那么这两个三角形相似。
推论六:如果一个三角形的两边和第三边上的中线与另一个三角形的对应部分成比例,那么这两个三角形相似。
发现相似题
与“如图,已知⊙O和⊙O′相交于A、B两点,过点A作⊙O′的切线交⊙O于点...”考查相似的试题有:
- 如图,在半径为6,圆心角为90°的扇形OAB的上,有一个动点P,PH⊥OA,垂足为H,△OPH的重心为G.(1)当点P在上运动时,线段GO、...
- 现有两根木棒,长度分别为30cm和40cm,若要订成一个直角三角形框架,那么所需的第三根木棒的长度可以是( )A.30cmB.40cmC...
- 有一个直角三角形,它的两边长是方程的两根,且第三条边长为5,求k的值?
- 若△ABC的三边a、b、c满足(a-b)(b2-2bc+c2)(c-a)=0,那么△ABC的形状是( )A.等腰三角形B.直角三角形C.等边三角形D.锐...
- 在等腰△ABC中,,则高的长为( )A.5B.10C.12D.
- 下列每组数分别表示三根木棒的长度,将它们首尾连接后,能摆成三角形的一组是A.1,2,6B.2,2,4C.1,2,3D.2,3,4
- 如图,在三角形纸片ABC中,AC=BC.把△ABC沿着AC翻折,点B落在点D处,连接BD,如果∠BAD=80°,则∠CBD的度数为 ▲ °.
- 如图,已知平行四边形ABCD的对角线相交于点O,延长AB到F,连接OF交BC于E,AB=a,BC=b,BF=c,求BE的长.
- 某生活小区的居民筹集资金1600元,计划在一块上、下底分别为10 m,20 m的梯形空地上种植花木,如图甲所示.(1)他们在△AMD和△B...
- 考虑下面4个命题:①有一个角是100°的两个等腰三角形相似;②斜边和周长对应相等的两个直角三角形全等;③对角线互相垂直且相等...