直线与圆的位置关系:
直线与圆的位置关系有三种：直线与圆相交，直线与圆相切，直线与圆相离。
（1）相交：直线和圆有两个公共点时，叫做直线和圆相交，这时直线叫做圆的割线，公共点叫做交点AB与⊙O相交，d<r；
（2）相切：直线和圆有唯一公共点时，叫做直线和圆相切，这时直线叫做圆的切线，这个唯一的公共点叫做切点。AB与⊙O相切，d=r。
（3）相离：直线和圆没有公共点时，叫做直线和圆相离,AB与圆O相离，d>r。（d为圆心到直线的距离）

圆锥：
以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转形成的面所围成的东西叫做圆锥体。该直角边叫圆锥的轴。

圆锥的组成构件：
①圆锥的高：圆锥的顶点到圆锥的底面圆心之间的距离叫做圆锥的高；
②圆锥的母线：圆锥的侧面展开形成的扇形的半径、底面圆周上点到顶点的距离。
③圆锥的侧面积：将圆锥的侧面沿母线展开，是一个扇形,这个扇形的弧长等于圆锥底面的周长,而扇形的半径等于圆锥的母线的长。
圆锥的侧面积就是弧长为圆锥底面的周长×母线/2；没展开时是一个曲面。
④圆锥有一个底面、一个侧面、一个顶点、一条高、无数条母线，且底面展开图为一圆形侧面展开图是扇形。
⑤圆锥侧面展开是一个扇形，已知扇形面积为二分之一rl。所以圆锥侧面积为二分之一母线长×弧长（即底面周长）。
另外，母线长等于底面圆直径的圆锥，展开的扇形就是半圆。
所有圆锥展开的扇形角度等于（底面直径÷母线）×180度。

圆锥的计算：
设圆锥底面圆的半径为r，母线长为l，n为圆心角度数
则圆锥的侧面积：，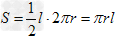
圆锥的全面积：S=S_侧+S_底=，
圆锥的体积：V=Sh=·πr2h
底面周长（C）=2πr=（nπl）/
h=根号（l²-r²）

特殊位置的点的坐标的特点：
1.x轴上的点的纵坐标为零；y轴上的点的横坐标为零。
2.第一、三象限角平分线上的点横、纵坐标相等；第二、四象限角平分线上的点横、纵坐标互为相反数。
3.在任意的两点中，如果两点的横坐标相同，则两点的连线平行于纵轴；如果两点的纵坐标相同，则两点的连线平行于横轴。
4.点到轴及原点的距离
点到x轴的距离为|y|； 点到y轴的距离为|x|；点到原点的距离为x的平方加y的平方的平方根；

对称点：
1.关于x轴成轴对称的点的坐标，横坐标相同，纵坐标互为相反数。（横同纵反）
2.关于y轴成轴对称的点的坐标，纵坐标相同，横坐标互为相反数。（横反纵同）
3.关于原点成中心对称的点的坐标，横坐标与横坐标互为相反数，纵坐标与纵坐标互为相反数。（横纵皆反）

点的符号：
横坐标 纵坐标
第一象限：（+，+）正正
第二象限：（-，+）负正
第三象限：（-，-）负负
第四象限：（+，-）正负
x轴正半轴：（+，0）
x轴负半轴：（-，0）
y轴正半轴：（0，+)
y轴负半轴： (0，-）
x轴上的点的纵坐标为0，y轴上的点的横坐标为0。
原点：（0，0）
注：以数对形式（x，y）表示的坐标系中的点（如2，-4），“2”是x轴坐标，“-4”是y轴坐标。

其他公式：
1.坐标平面内的点与有序实数对一一对应。
2. 一三象限角平分线上的点横纵坐标相等。
3.二四象限角平分线上的点横纵坐标互为相反数。
4.一点上下平移，横坐标不变，即平行于y轴的直线上的点横坐标相同。
5.y轴上的点，横坐标都为0。
6.x轴上的点，纵坐标都为0。
7.坐标轴上的点不属于任何象限。
8.一个关于x轴对称的点横坐标不变，纵坐标变为原坐标的相反数。反之同样成立。
9.一个关于原点对称的点横纵坐标均为原坐标相反数。
10.与x轴做轴对称变换时，x不变，y变
11.与y轴做轴对称变换时，y不变，x变
12.与原点做轴对称变换时，y与x都变